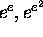 and
and 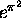
by
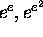 and
and 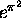
Abstract. We give two measures of simultaneous approximation
by algebraic numbers, the first one for the triple 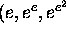 )
and the second one for
)
and the second one for 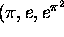 ).
We deduce from these measures two transcendence results which had been
proved in the early 70's by W.D. Brownawell and the author.
).
We deduce from these measures two transcendence results which had been
proved in the early 70's by W.D. Brownawell and the author.
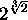 and
and 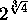 are algebraically
independent. At the same time, he proved that one at least of the three
numbers
are algebraically
independent. At the same time, he proved that one at least of the three
numbers 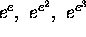 is transcendental
(see[G] Chap. III, ).
is transcendental
(see[G] Chap. III, ).
At the end of his book [S] on transcendental numbers, Th. Schneider
suggested that one at least of the two numbers 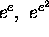 is transcendental; this was the last of a list of eight problems, and the
first to be solved, in 1973, by W.D. Brownawell [B] and M.Waldschmidt [W
1], independently and simultaneously. For this result they shared the Distinguished
Award of the Hardy-Ramanujan Society in 1986. Another consequence of their
main result is that one at least of the two following statements holds
true:
is transcendental; this was the last of a list of eight problems, and the
first to be solved, in 1973, by W.D. Brownawell [B] and M.Waldschmidt [W
1], independently and simultaneously. For this result they shared the Distinguished
Award of the Hardy-Ramanujan Society in 1986. Another consequence of their
main result is that one at least of the two following statements holds
true:
(i) The numbers e and 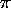 are algebraically independent
are algebraically independent
(ii)The number 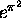 is
transcendental
is
transcendental
Our goal is to shed a new light on these results. It is hoped that our approach will yield further progress towards a solution of the following open problems:
(?) Two at least of the three numbers 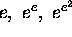 are algebraically independent.
are algebraically independent.
(?) Two at least of the three numbers 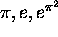 are algebraically independent.
are algebraically independent.
Further conjectures are as follows:
(?) Each of the numbers 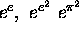 is transcendental
is transcendental
(?) The numbers e and 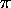 are algebraically independent.
are algebraically independent.
We conclude this note by showing how stronger statements are consequences of Schanuel's conjecture.
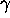 be a complex algebraic
number. The minimal polynomial of
be a complex algebraic
number. The minimal polynomial of 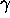 over Z Z is the unique polynomial
over Z Z is the unique polynomial
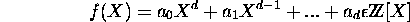
which vanishes at the point 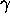 ,
is irreducible in the factorial ring
,
is irreducible in the factorial ring 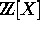 and has leading coefficient
and has leading coefficient 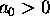 .
The integer
.
The integer 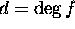 is the degree
of
is the degree
of 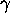 , denoted by
, denoted by 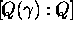 .
The usual height
.
The usual height 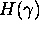 of
of  is defined by
is defined by
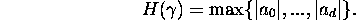
It will be convenient to use also the so-called Mahler's measure
of 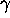 , which can be defined
in three equivalent ways. The first one is
, which can be defined
in three equivalent ways. The first one is
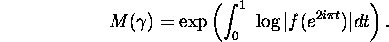
For the second one, let 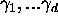 denote the complex roots of f, so that
denote the complex roots of f, so that
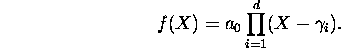
Then, according to Jensen's formula, we have
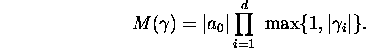
For the third one, let K be a number field (that is a subfield
of C| which is a Q/ -vector space of finite dimension [K:Q/ ]) containing 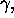 and let
and let 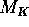 be the set of
(normalized) absolute values of K. Then
be the set of
(normalized) absolute values of K. Then
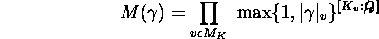
where 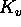 is the
completion of K for the absolute value v and
is the
completion of K for the absolute value v and 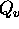 the topological closure of
the topological closure of 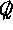 in
in 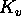 and
and 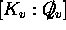 the local degree.
the local degree.
Mahler's measure is related to the usual height by
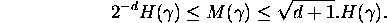
From this point of view it does not make too much difference to
use H or M, but one should be careful that d denotes
the exact degree of 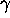 , not
an upper bound. We shall deal below with algebraic numbers of degree d
bounded by some parameter D.
, not
an upper bound. We shall deal below with algebraic numbers of degree d
bounded by some parameter D.
Definition. For an algebraic number 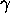 of degree d and Mahler's measure
of degree d and Mahler's measure 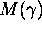 ,
we define the absolute logarithmic height
,
we define the absolute logarithmic height 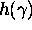 by
by
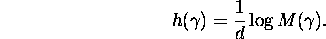
2.1. Simultaneous Approximation to 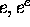 and
and 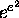
Theorem 1. There exists a positive absolute constant 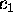 such that, if
such that, if 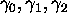 are algebraic
numbers in a field of degree D, then
are algebraic
numbers in a field of degree D, then
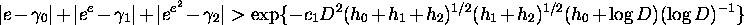
where 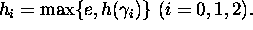
2.2. Simultaneous Approximation to 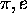 and
and 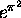
Theorem 2. There exists a positive absolute constant 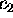 such that, if
such that, if 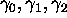 are algebraic
numbers in a field of degree D, then
are algebraic
numbers in a field of degree D, then
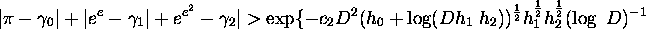
where 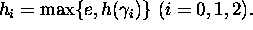
The following result is Théoréme 3.2 of [R-W 1]; see also Theorem 1.1 of [R-W 2].
Theorem 3. Let  be a complex number. The two following conditions are equivalent:
be a complex number. The two following conditions are equivalent:
(i) the number 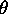 is transcendental.
is transcendental.
(ii) For any real number 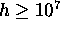 ,
there are infinitely many integers
,
there are infinitely many integers  for which there exists an algebraic number
for which there exists an algebraic number 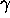 of degree d and absolute logarithmic height
of degree d and absolute logarithmic height 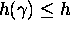 which satisfies
which satisfies
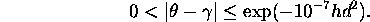
Notice that the proof of  is an easy consequence of Liouville's inequality.
is an easy consequence of Liouville's inequality.
3.2. Application to  and
and 
Corollary to Theorem 1. One at least of the two numbers 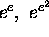 is transcendental.
is transcendental.
Proof of the corollary. Assume that the two numbers 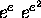 are algebraic, say
are algebraic, say  and
and  .
Then, according to Theorem 1, there exists a constant
.
Then, according to Theorem 1, there exists a constant 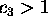 such that, for any algebraic number
such that, for any algebraic number 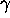 of degree
of degree 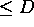 and height
and height 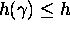 with
with 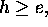
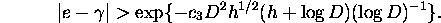
We now use Theorem 3 for 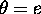 with
with 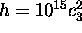 and derive a contradiction.
and derive a contradiction.
The proof of the following result is given in [R-W 1], Théoréme 3.1, as a consequence of Theorem 3 (see also [R-W 2] Corollary 1.2).
Corollary to Theorem 3. Let 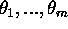 be complex numbers such that the field
be complex numbers such that the field 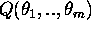 has tyranscendence degree 1 over Q. There exists a constant c > 0
such that, for any real number
has tyranscendence degree 1 over Q. There exists a constant c > 0
such that, for any real number  ,
there are infinitely many integers D for which there exists a tuple
,
there are infinitely many integers D for which there exists a tuple 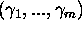 of algebraic numbers satisfying
of algebraic numbers satisfying
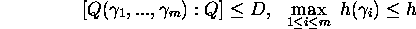
and
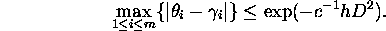
4.2. Application to 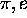 and
and 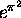
Corollary to Theorem 2. One at least of the two following
statements is true:
(i) The numbers e and 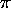 are algebraiclly independent.
are algebraiclly independent.
(ii) The number 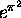 is transcendental.
is transcendental.
Remark. This corollary can be stated in an equivalent way as follows:
For any non constant polynomial 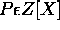 ,
the complex number
,
the complex number

is transcendental.
The idea behind this remark originates in [R].
Proof of the Corollary. Assume that the number 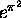 is algebraic. Theorem 2 with
is algebraic. Theorem 2 with 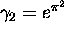 shows that there exists a constant
shows that there exists a constant 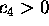 such that, for any pair
such that, for any pair 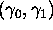 of algebraic numbers, if we set
of algebraic numbers, if we set
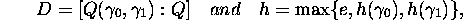
then
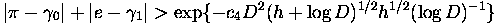
Therefore we dedeuce from the Corollary to Theorem 3 that the
field 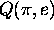 has transcendence
degree 2.
has transcendence
degree 2.
Schanuel's Conjecture. Let 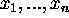 be Q-linearly independent complex numbers. Then, among the 2n numbers
be Q-linearly independent complex numbers. Then, among the 2n numbers
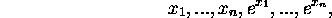
at least n are algebraically independent.
Let us deduce from Schanuel's Conjecture the following statement (which is an open problem):
(?) The 7 numbers
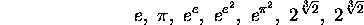
are algebraically independent.
We shall use Schanuel's cinjecture twice. We start with the numbers 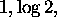 and
and 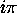 which are linearly
independent over Q because
which are linearly
independent over Q because 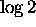 is irrational. Therefore, according to Schanuel's conjecture, three at
least of the numbers
is irrational. Therefore, according to Schanuel's conjecture, three at
least of the numbers
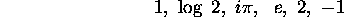
are algebraically independent. This means that the three numbers 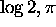 and e are algebraically independent. Therefore the 8 numbers
and e are algebraically independent. Therefore the 8 numbers
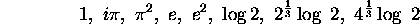
are Q-linearly independent. Again, Schanuel's conjecture implies that 8 at least of the numbers
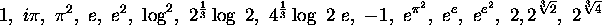
are algebraically independent, and this means that the 8 numbers
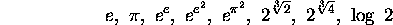
are algebraically independent.
ACKNOWLEDGEMENTS.
This research was performed in March/April 1998 while the author visited the Tata Institute of Fundamental Research under a cooperation program from the Indo-French Center IFCEPAR/CEFIPRA Research project 1601-2 << Geometry >>, The author wishes also to thank Professor K.Ramachandra for his invitation to the National Institute of Advanced Studies at Bangalore.
E-mail: miw@math.jussieu.fr
Received 28th March 1998
Accepted 30th April 1998.
Hardy-Ramanujan Journal
Vol.21 (1998) 35-36