Towards a nonlinear Schwarz's list*
The many facets of geometry: a tribute to Nigel Hitchin
J-P. Bourguignon, O. Garcia-Prada & S. Salamon (ed.s), Oxford University Press (2010) 210-236
This is basically the text of a survey talk, given at Hitchin's 60th birthday conference in 2006, concerning the search for and construction of algebraic solutions of the sixth Painlevé differential equation, which may be viewed as a nonlinear analogue of the Gauss
hypergeometric equation.
Both algebraic and transcendental methods are used and the story involves
affine Weyl groups, braid groups and cubic surfaces.
We will emphasize the interpretation of the sixth Painlevé equation as the explicit form of the simplest nonabelian Gauss-Manin connection, i.e. as a nonlinear differential equation 'coming from geometry', much as Picard-Fuchs equations
arise in the abelian case.
arXiv:0707.3374 July 2007
published version
(note that the TinyURL link in the reference Boalch 2006d to the
71pp of Cambridge slides has deprecated and should be replaced with that below)
A longer version of this talk was also given in Cambridge, September 2006:
Survey of the known algebraic solutions of Painlevé VI
Slides I,
Slides II,
for the two talks
I,
II,
(local copy in one file)
Slides of the original talk are here:
Painlevé, Klein and the icosahedron,
ICMAT Madrid, September 2006
* Lisovyy-Tykhyy (arXiv:0809.4873 September 2008) claim that the list of
this article is in fact complete (so there are no more than
the 45 equivalence classes of exceptional solutions that we completed the construction of).
The table of known (equivalence classes of) solutions (before it was proved to be complete by Lisovyy-Tykhyy) first appeared on p.18 of the 2006 Cambridge slides (before appearing at the end of arXiv:0707.3374):

Thus there are some infinite families plus 45 exceptional solutions.
The notions of equivalence used are discussed carefully in
sections 3,4 of this
paper.
The Klein solution was proved to exist in 2002,
as documented here, and then constructed explicitly
in 2003 in
this paper.
That paper also
proved that this solution really is sporadic
in the sense that it is not related to
any finite subgroup of SL2(C)
The 33 exceptional icosahedral solutions are rows 20-52 of the icosahedral list on p.14 of this paper.
The first 19 icosahedral solutions fit into one of the families, as explained in the article
(the first 10 correspond to the 10 icosahedral rows on Schwarz's original list, reproduced on p.2 of this paper).
The most difficult solution to construct explicitly was the
degree 24 genus one Valentiner solution
(in section 8 of this paper).
That computation was done overnight, running maple
on the Medicis computers at the Ecole Polytechnique in Paris,
via an ssh connection from my laptop on a post-doc's desk
in the Kobe University Math. Department, December 2004.
The remaining eight icosahedral solutions,
including the largest (genus seven) Painlevé curve,
were constructed explicitly in
this paper, and
the best way to understand the trick used here might be to look at p.69 of the Cambridge slides:
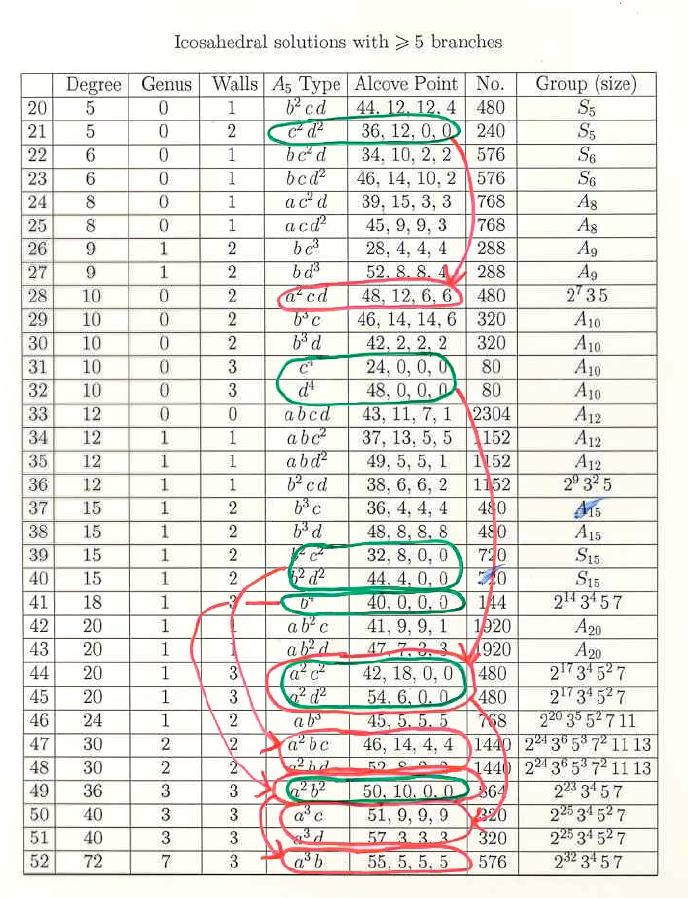
Note that this table lists equivalence classes of solutions, and this was essential to get a manageable list.
Recall the full table has 52 rows and this breaks up as:
52 = 10 + 9 + 33
where the first 10 are the braid group orbits of size one (corresponding to the 10 icosahedral rows on Schwarz's original list of algebraic solutions of the the Gauss hypergeometric equation) and the next 9 correspond to the non-exceptional solutions (living in one of the continuous families). The remaining 33 are the exceptional solutions listed above.
If we do the same counting before passing to equivalence classes we get
the following numbers:
3464 = 1216 + 464 + 1784.
Here 3464 is the number of braid group orbits of conjugacy classes of generating triples of the binary icosahedral group. It breaks up into the corresponding three case as above. Thus there are 1784 orbits of size >4 and this number then reduces to the 33 equivalence classes of exceptional orbits.
These numbers are computed from the table by dividing the column "No." by the orbit sizes.
For example:
1784 =
(480+240)/5
+
(576+576)/6
+
(768+768)/8
+
(288+288)/9
+
(480+320+320+80+80)/10
+
(2304+1152+1152+1152)/12
+
(480+480+720+720)/15
+
144/18
+
(1920+1920+480+480)/20
+
768/24
+
(1440+1440)/30
+
864/36
+
(320+320)/40
+
576/72.
(Recall that there are 26688 conjugacy classes of generating triples of the binary icosahedral group, by a theorem of P. Hall or by direct counting, and 26688 is partitioned into the 52 numbers in the "No." column of the full table).
The exceptional tetrahedral solution is the solution on the last row
(row 6) of the tetrahedral list on p.7 of
this paper.
The first 5 tetrahedral solutions fit into one of the families
(and the first 2 correspond to the 2 tetrahedral rows
on Schwarz's original list).
The 7 exceptional octahedral solutions are the last 7 rows (rows 7-13) of the octahedral list on p.11 of this paper.
The first 6 octahedral solutions fit into one of the families
(the first 2 correspond to the 2 octahedral rows
on Schwarz's original list).
The first genus one degree 18 "237" exceptional solution was constructed
in v1 (p.15) of
this paper, and the link to the other two Galois siblings of it
is on p.22 of the final version (v2) of this paper.
In fact up to isomorphism there is only one degree 4 continuous family
(this was pointed out by Cantat-Loray, and is stated correctly on the last page of arXiv:0707.3374).

