Program by Eyal Markman

The outlines below of the content of the lectures are uneven in their level of detail. Some are brief, and would just ask to cover a certain section. Others are more detailed, when the content is to diverge from the reference suggested in order to simplify it, or in case the translation from the material in the text suggested to the content of the lecture is less obvious. So a longer description does not mean more material to be covered. When I suggest to state a result and omit the proof it means that the time plan for the lecture does not include time for the proof. If you feel that you do have time, by all means, include any proof you wish.

Notation: Given a free abelian group $V$ and a field $K$, set $V_K:=V\otimes_\mathbb{Z} K$. Similarly, if $V$ is a vector space over $\mathbb{Q}$ and $K$ is a field of characteristic $0$ we set $V_K:=V\otimes_\mathbb{Q} K$. Given an abelian variety $A$ we set $\operatorname{End}_\mathbb{Q}(A):=\operatorname{End}(A)\otimes_\mathbb{Z}\mathbb{Q}$ and refer to it as the ring of rational endomorphisms of $A$.

Program (pdf version)

1. The Hodge conjecture for abelian varieties

The main reference is Sections 1 to 4 of [13] (for complex multiplication by quadratic imaginary number fields), which is easier to read than the original paper of Weil "Abelian varietiens and the Hodge ring". A generalization for CM-fields is discussed in [10].

1. Survey the first 4 sections of [13] ending with the overview of results (Weil's Theorem, The reduction of the Hodge conjecture for abelian $4$-folds to abelian varieties of Weil type due to Moonen-Zarhin, Scheon's Theorem). This should be the content of most of the lecture.
   
   
2. State the main result of [22] that the Weil classes on abelian sixfolds of split Weil type are algebraic.
   
   
3. State Tankeev theorem that the Hodge ring on simple abelian varieties of prime dimension is generated by divisor classes.
   
   
4. State the theorem of Moonen-Zarhin (Th. 0.2 in [26]) about the generation of the Hodge ring of non-simple abelian $5$-folds by divisor classes and pull back of Weil classes from quotient abelian $4$-folds.Conclude that the Hodge conjecture holds for abelian varieties of dimension $\leq 5$.

2. Abelian varieties of Weil type

This lecture consists of a detailed exposition of Section 5 of [13].

1. State and prove Lemma 5.2 on the cohomology of abelian varieties of Weil type. The polarization, the hermitian form, its discriminant, and the definition of the two dimensional space of Hodge Weil classes $HW(A,\eta)$ on an abelian variety of Weil type $(A,\eta:K\rightarrow \operatorname{End}_\mathbb{Q}(A))$
   
   
2. Describe the construction of the $n^2$-dimensional family of polarized abelian varieties of Weil type ($H_n$ in the notation of [13]), the transitive $SU(n,n)$ action, and the complex structure.
   
   
3. Go over Example 5.12 in [13].
   
   
4. Emphasize that up to isogeny the three discrete invariants $\dim(A)$, $K$, and \[\det(A,\eta,h)\in \mathbb{Q}^\times/Nm(K^\times)\] determine the connected component of moduli up to isogenies, by the main result of reference [L] in [13]. In other words, given a polarized abelian variety of Weil type $(A,\eta,h)$ and any connected component of moduli with the same values of these three discrete invariants, the component contains the isomorphism class of a polarized abelian variety of Weil type $(A',\eta',h')$,such that there exists an isogeny between $A$ and $A'$ inducing a $K$-linear isomorphism of $H_1(A,\mathbb{Q})$ and $H_1(A',\mathbb{Q})$ compatible with the hermitian forms associated to $(\eta,h)$ and $(\eta',h')$.
   
   
5. Conclude that it suffices to prove the algebraicity of the Weil classes for all polarized abelian varieties of Weil type in one component, for each value of these three discrete invariants.

3. Mumford-Tate groups

Present Section 6 of [13]. See also the survey paper of Griffiths [14]. The main results are Th. 6.11 in [13] that the Special Mumford Tate group of the general polarized abelian variety of Weil type is $SU_H$, and Th. 6.12 in [13] about the Hodge ring of the general polarized abelian variety of Weil type.



4. Schoen's proof of the algebraicity of the Weil classes on abelian fourfolds of Weil type, case of $\mathbb{Q}(\sqrt{-3})$

C. Schoen proved the algebraicity of the Weil classes on abelian fourfolds of split Weil type with complex multiplication by $\mathbb{Q}(\sqrt{-3})$ in [29]. He claimed in this paper to have proven it for all abelian fourfolds of Weil type, but corrected this assertion and proved it in [30] for abelian sixfolds of split Weil type with complex multiplication by $\mathbb{Q}(\sqrt{-3})$, thereby proving it for all abelian fourfolds. Similar results were obtained for $\mathbb{Q}(\sqrt{-1})$ in [19]. Present the sketch of the proof of the algebraicity of the Weil classes on abelian fourfolds of split Weil type with complex multiplication by $\mathbb{Q}(\sqrt{-3})$ and $\mathbb{Q}(\sqrt{-1})$ from Sec. 7 in [13]. I suggest that you concentrate on the case $\mathbb{Q}(\sqrt{-3})$ and expand the presentation by referring to [29].



5. Semiregularity and deformations

The most important reference is [2]. We need however just the statement of their semiregularity theorem. Most of the effort will be to generalize it to twisted sheaves Sec. 7 in [22] (a generalization was discussed also in [28] and [17]).

1. A discussion of Chern classes, Chern characters, and some basic properties.
   
   
2. Define the Atiyah class $at_E$ of a coherent sheaf $E$ over an $N$-dimensional smooth projective variety (or Kähler manifold) $M$ using the universal Atiyah class (see Sec. 10.1 in [16] and (7.3.2) in [22]).
   
   
3. Relate the Chern character to the trace of the exponential Atiyah class (Sec. 10.1 in [16]).
   
   
4. Define the semiregularity map \[ \sigma_E: \operatorname{Ext}^2(E,E)\rightarrow \oplus_{q=0}^{N-2}H^{q+2}(M,\Omega^q_M) \] and the commutative diagram of Cor. 4.3 in [2] (displayed in Diagram (7.1.2) in [22]).
   
   
5. Explain that $at_E\rfloor :H^1(M,TM)\rightarrow \operatorname{Ext}^2(E,E)$ is the obstruction homomorphism to lifting classes in $H^1(TM)$ to infinitesimal deformations of the pair $(M,E)$ (see [31]). For simplicity, you may explain the latter only for a locally free sheaf $E$, in which case the first order deformations of $(M,E)$ are parametrized by $H^1(\mathit{Diff}^1(E)_s)$, where $\mathit{Diff}^1(E)_s$ is the sheaf of first order differential operators with scalar symbol. The latter fits in the short exact sequence \begin{equation} \tag{1} 0\rightarrow \mathcal{E}\mathit{nd}(E)\rightarrow \mathit{Diff}^1(E)_s \rightarrow TM\rightarrow 0 \end{equation} and contraction with $at_E$ is the connecting homomorphism from $H^1(TM)$ to $H^2(\mathcal{E}\mathit{nd}(E))\cong\operatorname{Ext}^2(E,E)$. Note that the coherent sheaf of first order differential operators $\mathit{Diff}^1(E)$ is isomorphic to $\mathcal{H}\mathit{om}(j^1(E),E)$, where $j^1(E)$ is the first jet bundle of $E$. (Let $\mathcal{I}_{\Delta}$ be the ideal sheaf of the diagonal $\Delta\subset M\times M$. The first order neighborhood $\Delta_1$ of the diagonal is the scheme with structure sheaf $\mathcal{O}_{\Delta_1}:=\mathcal{O}_{M\times M}/\mathcal{I}_{\Delta}^2$. The first jet bundle is $j^1(E):=\pi_{2,*}(\pi_1^*(E))$, where $\pi_i:\Delta_1\rightarrow M$, $i=1,2$, is the restriction to $\Delta_1$ of the projection $M\times M\rightarrow M$ onto the $i$-th factor.) Applying $R\mathcal{H}\mathit{om}(\bullet,E)$ to the short exact sequence \[ 0\rightarrow E\otimes\Omega^1_M\rightarrow j^1(E)\rightarrow E\rightarrow 0 \] we get the short exact \[ 0\rightarrow \mathcal{E}\mathit{nd}(E)\rightarrow \mathit{Diff}^1(E) \rightarrow \mathcal{E}\mathit{nd}(E)\otimes TM\rightarrow 0. \] The short exact sequence (1) is the pullback of the one above via the homomorphism $TM\rightarrow \mathcal{E}\mathit{nd}(E)\otimes TM$ of tensoring with the identity endomorphism of $E$. A local splitting of the short exact sequence (1) is given by a local holomorphic connection. The above can be generalized to any coherent sheaf $E$ by replacing $E$ by a complex of locally free sheaves. Local holomorphic connections of such complexes are discussed in Sec. 10.1 of [16].
   
   
6. Interpret the injectivity of the semiregularity map $\sigma_E$ as equality of the kernels of two arrows in Diagram (7.1.2) in [22]. Then state it as the equivalence of the vanishing of two obstractions, where the vanishing of $\xi\rfloor ch(E)$, for $\xi\in H^1(TM)$, is the condition for $ch(E)$ to remain of Hodge type along $\xi$, by Griffiths Transversality (Theorem 10.21 in [34]).

6. The semiregularity theorem and its generalization to twisted sheaves

1. State the Buchweitz-Flenner Semiregularity Theorem Th. 5.1 in [2].
   
   
2. The Semiregularity Theorem enables us to deform a coherent sheaf $E$ flatly to every fiber over an open analytic neighborhood $U$ of a point in the base $B$ of the family. Hence, $ch(E)$ remains algebraic in the fibers over points of $U$ (assuming now that the fibers are projective). Point out that if the base $B$ of the family is smooth and connected, then $ch(E)$ remains in fact algebraic in every fiber (over the whole base), since the locus in the base, where a class remains algebraic, is a countable union. Under the aditional assumption that $B$ is quasiprojective, that locus is in fact a closed analytic subset (Sec. 17.3.1 in [32]) and even algebraic, by a theorem of Cattani-Deline-Kaplan of closed complex analytic subvarieties of $B$ (see Sec. 4.2 in [33]).
   
   
3. 1. Prove that every simple sheaf on a $K3$ or abelian surface is semiregular.
      
      
   2. Use the main result of [11], that the minimal class $\Theta^3/3!$ on the generic principally polarized abelian fourfold $(A,\Theta)$ is not algebraic, to conclude that the ideal sheaf $\mathcal{I}_{AJ(C)}$ of the Abel-Jacobi image of a curve $C$ of genus $4$ in its Jacobian $\operatorname{Pic}^1(C)$ is not semiregular.
      
      
   3. Point out that the codomain of the semiregularity map $\sigma_E$ has a fixed dimension $D:=\sum_{q=0}^{N-2}h^{q,q+2}(M)$, so as soon as $\dim(\operatorname{Ext}^2(E,E))>D$, the sheaf $E$ can not be semiregular in the strict sense of [2].
   
   
   
4. Let $E$ be a rank $r>0$ coherent sheaf. Explain that the condition that $ch(E)$ remains a Hodge class over the base (which appears in the Semiregularity Theorem) is equivalent to the conjunction of the following two independent conditions.
   
   
   1. $c_1(E)$ remains of Hodge type, and
   2. $\kappa(E):=ch(E)\exp\left(-c_1(E)/r\right)$ remains of Hodge type over the base.
   
   We would like to strengthen the theorem, by dropping the condition on $c_1(E)$ and deforming instead a related, possibly twisted, coherent sheaf with vanishing first Chern class. The simplest case is the following.

   Example. Let $E$ be a rank $r$ coherent sheaf with the property that $c_1(E)/r\in H^{1,1}(M,\mathbb{Q})$ is in fact integral, so that $\det(E)\cong L^r$, for some line bundle $r$ and $E\otimes L^{-1}$ has trivial determinant. In this case $\kappa(E)=ch(E\otimes L^{-1})$, $E$ is semiregular if and only if $E\otimes L^{-1}$ is, and if in addition $\kappa(E)$ remains of Hodge type, then the semiregularity theorem applies to $E\otimes L^{-1}$.

5. Define twisted coherent sheaves. The elementary language of [22] follows [4] avoiding the language of stacks.
   
   
6. Present Construction 7.3.3 in [22] of the twisted sheaf with trivial determinant line-bundle associated to a coherent sheaf of positive rank.
   
   
7. Define the Atiyah class of a twisted sheaf and its Chern character (Def. 7.3.5, 7.3.6 in [22], defined in other texts earlier, e.g., in [20]). Relate the Chern character of the twisted sheaf in Construction 7.3.3 in [22] to that of the original untwisted coherent sheaf (Lemma 7.3.7 [22]).
   
   
8. State Conjecture 7.3.9 in [22]. If time permits, sketch the proof of the Conjecture in the case of abelian varieties found in Sec. 7.4 of [22]. (I can provide notes for a simplified proof of a slightly less general statement, suggested by Footnote 19 in [22], which suffices for our application).

7. The Clifford algebra and the spin group associated to an abelian variety

The best reference on Clifford algebras and spin groups for our purpose is [8]. The paper [12] includes an excellent summary of the basic facts we need, but it does not contain the material on pure spinors we need later. Let $X$ be an $n$-dimensional abelian variety and set $\hat{X}:=\operatorname{Pic}^0(X)$. For motivation, mention that the semiregular sheaf we need will be constructed over $X\times\hat{X}$, where $X$ is an abelian surface [21] or the Jacobian of a curve of genus $3$ [22], and that we hope to find examples for all higher dimensional abelian varieties. Point out that $V:=H^1(X,\mathbb{Z})\oplus H^1(\hat{X},\mathbb{Z})$ has a natural symmetric even unimodular bilinear pairing $(\bullet,\bullet)_V$ given in (1.2.2) in [22].

1. Define the Clifford algebra $C(V)$ over $\mathbb{Z}$ as in [12]. One needs to use the quadratic form $Q(\bullet)=\frac{1}{2}(\bullet,\bullet)_V$ and not the bilinear pairing, as was unfortunately done in early versions of Sec. 2.1 in [22], in order to avoid two-torsion in $C(V)$. Define the Clifford group $G(V)$ and its subgroup $\operatorname{Spin}(V)$. Define the norm homomorphism and its kernel $SO_+(V_\bullet)$, for $\bullet=\mathbb{Z}$ or a field, where $V_\bullet:=V\otimes_\mathbb{Z}\bullet$. Point out that $SO_+(V_\bullet)$ is the image of $Spin(V_\bullet)$ in $SO(V_\bullet)$. See II.2.3 in [8] in the field case (in [8] $SO(V)$ is denoted by $G^+$ and $SO_+(V)$ by $G^+_0$.), and over $\mathbb{Z}$, by Cor. 5.1 in [21], which exhibits generators for $SO_+(V)$ which clearly belong to the image of the homomorphism $\rho$ in Eq. (2) below. Set $S:=H^*(X,\mathbb{Z})$. Define the isomorphism \[ m:C(V)\rightarrow \operatorname{End}(S)\] and the two half spin representations $S^+:=H^{ev}(X,\mathbb{Z})$ and $S^-:=H^{odd}(X,\mathbb{Z})$ of $\operatorname{Spin}(V)$. Use the notation \begin{eqnarray} \nonumber m : \operatorname{Spin}(V)&\rightarrow & GL(S), \\ \tag{2} \rho : \operatorname{Spin}(V) & \rightarrow & SO^+(V) \end{eqnarray} for the spin and vector representations.
   
   
2. For motivation (to be expanded in lecture 10) point out the following. Let $\operatorname{Aut}(D^b(X))$ be the group of isomorphism classes of autoequivalences of the derived category of coherent sheaves on a projective variety $X$. The group $\operatorname{Aut}(D^b(X))$ acts on $H^*(X,\mathbb{Q})$, not preserving the grading but preserving the Mukai pairing (see (1.2.3) in [22] for the case of abelian varieties, [5] in general), and it acts by conjugation on its identity component. When $X$ is an abelian variety, $\operatorname{Aut}(D^b(X))$ preserves the integral structure $H^*(X,\mathbb{Z})$ and the identity component of $\operatorname{Aut}(D^b(X))$ is $X\times\hat{X}$, where $\hat{X}:=\operatorname{Pic}^0(X)$. Note that $H^*(X\times\hat{X},\mathbb{Z})$ is the exterior algebra $\wedge^*V$ of the vector representation $V$. Orlov proved that the action of $\operatorname{Aut}(D^b(X))$ on $H^*(X,\mathbb{Z})$ and on $H^*(X\times\hat{X},\mathbb{Z})$ both factor through a homomorphism $\operatorname{Aut}(D^b(X))\rightarrow \operatorname{Spin}(V)$ via the spin and vector representations of the latter. Orlov proved that one gets the short exact sequence \begin{equation} \tag{3} 0\rightarrow X\times\hat{X}\times\mathbb{Z}\rightarrow \operatorname{Aut}(D^b(X))\rightarrow \operatorname{Spin}_{Hdg}(V)\rightarrow 0, \end{equation} where $\operatorname{Spin}_{Hdg}(V)$ is the subgroup of $\operatorname{Spin}(V)$ preserving the Hodge structure of $V$ and the factor $\mathbb{Z}$ corresponds to even shifts (the shift [$1$] maps to $-1$ in $\operatorname{Spin}(V)$). This is the way Orlov's results are presented in Prop. 4.3.7 and Cor. 4.3.9 in [12]. This explains the central role spin groups play in the geometry of abelian varieties.
   
   
3. The way we relate the vector and spin representations of $\operatorname{Spin}(V_\mathbb{C})$ is via Chevalley's theory of pure spinors [8]. Let $IGr(2n,V_\mathbb{C})$ be the grassmannian of maximal isotropic subspaces of $V_\mathbb{C}$. It has two connected components (when $X$ is an elliptic curve, $IGr(2,V_\mathbb{C})=\mathbb{P}^1\coprod\mathbb{P}^1$ corresponding to the two rulings of the quadric surface in $\mathbb{P}(V_\mathbb{C})$ cut out by the quadratic form of $V_\mathbb{C}$ associated to the symmetric bilinear pairing). So $IGr(2n,V_\mathbb{C})=IGr_+(2n,V_\mathbb{C})\coprod IGr_-(2n,V_\mathbb{C})$ in general. Describe the $\operatorname{Spin}(V)$-equivariant embedding \[ \ell:IGr(2,V_\mathbb{C}) \rightarrow \mathbb{P}(S_\mathbb{C}) \] mapping $IGr_+(2n,V_\mathbb{C})$ into $\mathbb{P}(S^+_\mathbb{C})$ and $IGr_-(2n,V_\mathbb{C})$ into $\mathbb{P}(S^-_\mathbb{C})$ (see III.1.5 in [8]. The variety $\ell(IGr_+(2n,V_\mathbb{C}))$ is called the even spinorial variety. Include the formula for the line $\ell_W$ of pure spinors in $S_\mathbb{C}$ corresponding to a maximal isotropic subspace $W\subset V_\mathbb{C}$ \[ \ell_W=\{\lambda\in S_\mathbb{C} \ : \ w\wedge \lambda + \theta\rfloor\lambda =0, \ \forall (w,\theta)\in W\}. \] Note that this formula also determine the maximal isotropic subspace $W$ associated to a pure spinor $\lambda\in S_\mathbb{C}$. Check that $1\in H^0(X)$ and $[pt]\in H^{2n}(X)$ are pure spinors and $\ell_{H^1(\hat{X})}=H^0(X)$ and $\ell_{H^1(X)}=H^{4n}(X)$.
   
   
4. Mention that the spinorial variety is $(2n^2-n)$-dimensional, where $n=\dim(X)$. When $X$ is an abelian surface, the even spinorial variety is the $6$-dimensional quadric in $\mathbb{P} H^{ev}(X,\mathbb{C})$ cut out by the Mukai pairing. When $n=3$, the $31$-dimensional $\mathbb{P} H^{ev}(X,\mathbb{C})$ is equal to the secant variety to the $15$-dimensional even spinorial variety. When $n\geq 4$, the $(4n^2-2n+1)$-dimensional secant variety is a proper subvariety of the $(2^{2n-1}-1)$-dimensional $\mathbb{P}(S^+_\mathbb{C})$.
   
   
5. Mention that when $\dim(X)=3$, the subring $[\operatorname{Sym}^*(S^+_\mathbb{Q})^*]^{\operatorname{Spin}(V_\mathbb{Q})}$, of $\operatorname{Spin}(V_\mathbb{Q})$-invariant polynomials in the homogeneous coordinate ring of $\mathbb{P}(S^+_\mathbb{Q})$, is a polynomial ring $\mathbb{Q}[J]$ generated by a single polynomial $J$ of degree $4$ (the Igusa quartic). The zero locus of $J$ is the tangential variety $\mathbb{P}(T\ell(Gr_+(6,V_\mathbb{Q})))$ (see [18] and Sec. 10 in [22]). Let $w\in S^+_\mathbb{Q}$. If $J(w)\neq 0$, then there exists through $w$ a unique secant and the value $J(w)$ determines the field of definition of the points of intersection of the secant with the spinorial variety (and so the field of definition of the corresponding maximal isotropic subspaces of $V_\mathbb{C}$). If $J(w)>0$, then the field of definition is the imaginary quadratic number field $K:=\mathbb{Q}\left(\sqrt{-J(w)}\right)$ (see Lemma 10.2.1 in [22]). The complex multiplication $\eta_P:K\rightarrow \operatorname{End}_\mathbb{Q}(X\times\hat{X})$ to be constructed below from the secant $P$ through $w$ will involve this field $K$.
   
   
6. Present the example of the rational $K$-secant in formula (1.2.4) in [22]. It is a $2$-dimensional subspace $P\subset S^+_\mathbb{Q}$, such that $\mathbb{P}(P_K)$ is secant to the even spinorial variety in $\mathbb{P}(S^+_K)$, for each imaginary quadratic number fields $K$.

8. Polarized abelian varieties of Weil type from $K$-secants

A general Strategy for the proof of the algebraicity of the Weil classes: Let $X$ be an abelian $n$-fold. Let $d$ be a positive integer and set $K:=\mathbb{Q}(\sqrt{-d})$. Choose a $2$-dimensional subspace $P\subset S^+_\mathbb{Q}$, non-degenerate with respect to the Mukai pairing and spanned by Hodge classes, such that $\mathbb{P}(P_\mathbb{C})$ intersects the spinorial variety $IGr_+(2n,V_\mathbb{C})$ at two complex conjugate points defined over $K$, but not over $\mathbb{Q}$. Our goal in the rest of the lectures is to carry out for $n=3$ the following program. (With the exception of the semiregularity Condition (2a), we will carry the program for all $n$.)

1. Construct a complex multiplication $\eta_P:K\rightarrow \operatorname{End}_\mathbb{Q}(X\times\hat{X})$, such that the two maximal isotropic subspaces associated to the two pure spinors $\mathbb{P}(P_K)\cap IGr(2n,V_K)$ are associated to the two eigenspaces $W_1$ and $W_2$ of $\eta_P$. Construct also an $\eta_P$-compatible polarization $h_P$, so that $(X\times\hat{X},\eta_P,h_P)$ is a polarized abelian variety of Weil type.
   
   
2. Construct over $X\times\hat{X}$ a coherent sheaf $E$ of positive rank $r$, such that
   1. $E$ is semiregular (possibly only in an equivariant sense with respect to a subgroup $G\subset X\times\hat{X}$ of translations, so that it descends to the isogenous abelian variety $Y:=(X\times\hat{X})/G$ as a semiregular sheaf; note that $H^1(Y,\mathbb{Q})=H^1(X,\mathbb{Q})$, $h_P$ determines a polarization $\bar{h}_P$ on $Y$, and $(Y,\eta_P,\bar{h}_P)$ is a polarized abelian variety of Weil type).
      
      
   2. The class $\kappa(E):=ch(E)\exp(-c_1(E)/r)$ remains of Hodge type over every deformation of $(X\times\hat{X},\eta_P,h_P)$ as a polarized abelian variety of Weil type.
      
      
   3. The graded summand $\kappa_n(E)$ and $h^n$ are linearly independent.

The semiregularity theorem implies that $E$ deforms to a twisted coherent sheaf $E'$ over any deformation $(A,\eta,h)$ of $(X\times\hat{X},\eta_P,h_P)$. Hence, $\kappa_n(E')$ is algebraic. Weil's result from Lecture 2, that $\dim H^{n,n}(A')=3$ for the generic abelian variety of Weil type, combines with Condition (2b) to imply that $\kappa_n(E')$ belongs to $\operatorname{span}\{h^n\}\oplus HW(A,\eta)$. Condition (2c) implies that there exists $t\in\mathbb{Q}$, such that $\kappa_n(E)-th^n$ is a non-zero algebraic class in $HW(A,\eta)$. Now $K$ acts on $H^{2n}(A,\mathbb{Q})$ via algebraic correspondences and $HW(A,\eta)$ is a $1$-dimensional $K$-subspace. Hence, every class in $HW(A,\eta)$ is algebraic.

1. Define the group $\operatorname{Spin}(V_K)_{\ell_1,\ell_2}$, the characters $\det_i$, and the group $\operatorname{Spin}(V_\mathbb{Q})_P$ associated to a $K$-secant $P$. State Lemmas 2.2.1 and 2.2.2 in [22]. There is a misprint in Lemma 2.2.2 in [22], the group should be $SL_{2n}(K)$. Note that $\operatorname{Spin}(V_\mathbb{Q})_P$ will be identified with the Mumford Tate group of the generic polarized abelian variety of Weil type from Lecture 3.
   
   
2. State and prove Lemma 2.2.6 in [22] stating that if the two dimensional subspace $P\subset S^+_K$ is spanned by Hodge classes, where $\mathbb{P}(P)$ a $K$-secant line, then the the two maximal isotropic subspaces $W_1$ and $W_2$ satisfy the Hodge theoretic condition on the eigenspaces of the complex multiplication from the definition of an abelian variety of Weil type.
   
   
3. State and prove Lemma 2.2.7 in [22] about the $\operatorname{Spin}(V)_P$-invariant subring $H^*(X\times\hat{X},\mathbb{Q})^{\operatorname{Spin}(V)_P}$. Conclude that a class $\gamma$ in $H^{n,n}(X\times\hat{X},\mathbb{Q})$ remains algebraic under every deformation of $(X\times\hat{X},\eta_P,h_P)$ as a polarized abelian variety of Weil type, if and only if $\gamma$ is $\operatorname{Spin}(V)_P$-invariant. Restate Condition (2b) of the general strategy in this language.

Next we relate the construction of the period domains of polarized abelian varieties of split Weil type (Weil's construction of these $n^2$-dimensional moduli spaces from Lecture 3) to $K$-secants. This will achieve Step 1 of the above strategy.

1. Cover the construction of the complex multiplication $\eta:K\rightarrow \operatorname{End}_\mathbb{Q}(X\times\hat{X})$ and the $\eta$-compatible polarization $h$ of Prop. 2.4.4 in [22] carried out in Sec. 2.4 of [22].
   
   
2. Show that $\operatorname{Spin}(V_\mathbb{Q})_P$ preserves a $K$-valued hermitian form $H$ and is isomorphic to $SU(V_\mathbb{Q},H)$ (Lemma 3.1.2 in [22]).
   
   
3. Show that $(X\times\hat{X},\eta,h)$ is of split Weil-type, i.e., that $\det(X\times\hat{X},\eta,h)$ is the coset of $(-1)^n$ in $\mathbb{Q}^\times/Nm(K^{\times})$, see Lemma 3.1.3 in [22]. Note that this is equivalent to $H^1(X\times\hat{X},\mathbb{Q})$ admitting a $K$-subspace of half the dimension isotropic with respect to the Hermitian form. A verification of this property (and so a different proof of the split Weil-type property) is given in 11.1.2 of [23].
   
   
4. Show that the adjoint orbit of the complex structure $I_{X\times\hat{X}}$ in $\operatorname{Spin}(V_\mathbb{R})_P$ is a period domain for abelian varieties of Weil type (sections 3.2 and 4 of [22]).

9. Equivalences of derived categories of coherent sheaves

1. Present in detail the basic facts about equivalences of derived categories of coherent sheaves on smooth projective algebraic varieties following Section 4.1 of [12] (see also Sec. 5 in [22]).
   
   
2. Define Mukai's derived equivalence $\Phi_\mathcal{P}:D^b(X)\rightarrow D^b(\hat{X})$ associated to the Poincaré line bundle $\mathcal{P}$ over $X\times\hat{X}$.
   
   
3. State and prove Prop. 4.2.2.1 in [12] relating the cohomological isomorphism associated to Mukai's equivalence to Poncaré duality (see also Lemma 9.23 in [15]).
   
   
4. State Exercise 9.21 in [15] and prove it if time permits.
   
   
5. If time permits, which is very unlikely, briefly mention some of the results in Sec. 9.3 of [15]. The convolution product $*:D^b(\hat{X})\times D^b(\hat{X})\rightarrow D^b(\hat{X})$ corresponds to the tensor product on $D^b(X)$ via Mukai's equivalence. We will not use the convolution product.

10. Chevalley's isomorphism and Orlov's derived equivalence

The general strategy presented in Lecture 7 calls for a coherent sheaf $E$ on $X\times\hat{X}$, such that $\kappa(E)$ remains a Hodge class on every deformation of $(X\times\hat{X},\eta_P,h_P)$, where $P\subset S^+_\mathbb{Q}$ is a $K$-secant, $\eta_P:K\rightarrow \operatorname{End}_\mathbb{Q}(X\times\hat{X})$ the complex multiplication associated to $P$, and $h_P$ the polarization associated to $P$. We have seen that $\operatorname{Spin}(V_\mathbb{Q})_P$ is the special Mumford Tate group of the generic deformation of $(X\times\hat{X},\eta,h)$ (by deforming the complex structure in the adjoint orbit of $I_{X\times\hat{X}}$ in $\operatorname{Spin}(V_\mathbb{R})_P$), so we need $\kappa(E)$ to be $\operatorname{Spin}(V)_P$-invariant. If $F_1$ and $F_2$ are two coherent sheaves on $X$ with $ch(F_i)$ in the secant $P$, then the Chern character of the sheaf $F_1\boxtimes F_2:=\pi_1^*F_1\otimes \pi_2^*F_2$ over $X\times X$ is $\operatorname{Spin}(V)_P$-invariant with respect to the diagonal action of $\operatorname{Spin}(V)$ on $H^*(X)\otimes H^*(X)$. If we can find an equivalence of derived categories $D^b(X\times X)\cong D^b(X\times\hat{X})$, which induces a $\operatorname{Spin}(V)$-equivariant isomorphism $H^*(X\times X,\mathbb{Z})\cong H^*(X\times\hat{X},\mathbb{Z})$, it would transform $F_1\boxtimes F_2$ to an object with a $\operatorname{Spin}(V)_P$-invariant Chern character. Such an equivalence does not exist. In this lecture we recall that Orlov found an equivalence, which induced cohomology isomorphism is sufficiently close to being $\operatorname{Spin}(V)$-equivariant, so that the transpose of $F_1\boxtimes F_2$ has a $\operatorname{Spin}(V)_P$-invariant $\kappa$ class.

1. Define Chevalley's isomorphism \[ \tilde{\varphi}: H^*(X\times X,\mathbb{Z})=S\otimes_\mathbb{Z} S\rightarrow \wedge^*V=H^*(X\times\hat{X},\mathbb{Z}) \] (see Eq. (2.3.2) in [22]). Point out that it is not $\operatorname{Spin}(V)$-equivariant, but it preserves a filtration on $\wedge^*V$ and induces $\operatorname{Spin}(V)$-equivariant isomorphisms of the graded pieces.



2. The goal of the rest of the lecture is to lift Chevalley's isomorphism $\tilde{\varphi}$ to the level of derived categories and study its properties.



3. Introduce the isomorphism $\phi$ in Eq. (1.2.5) in [22] (a composition of $\tilde{\varphi}$ with two standard automorphisms).



4. Define Orlov's equivalence \begin{equation} \tag{4} \Phi:D^b(X\times X)\rightarrow D^b(X\times\hat{X}) \end{equation} from Sec. 1.3 in [22]. Good references include [12] and [15]. Point out that $\Phi^{-1}$ maps the sky-scraper sheaf of a point $(a,L)\in X\times\hat{X}$ to the Fourier-Mukai kernel in $D^b(X\times X)$ of the derived equivalence $\tau_x^*(\bullet)\otimes L:D^b(X)\rightarrow D^b(X)$ (see section 4.2.4 of [12]).



5. The following comment is to be skipped in the lecture. It answers the question: How the hell did Orlov's equivalence got entangled with the algebraicity of the Weil classes? One may ask even why do we define the complex multiplication on the abelian variety $X\times\hat{X}$ and not on $X\times X$. Note that the simplest way to introduce complex multiplication is not on $X\times\hat{X}$, but rather on $X\times X$ by sending $\sqrt{-d}$ to the rational endomorphism $\left(\begin{array}{cc}0 & 1_X\\-d_X & 0\end{array}\right)$, where $d_X$ is $d$ times the identity endomorphism of $X$, as in Example 5.12 in [13].
   
   O'Grady was the first to realize the relationship between abelian fourfolds of Weil type and moduli spaces of sheaves on abelian surfaces [27]. Given a moduli space $M:=M(v)$ of stable sheaves with Chern character $v$ on an abelian variety $X$ we have a morphism $a:X\times \hat{X}\rightarrow \operatorname{Aut}(M)$ sending $(x,L)$ to the automorphism $\tau_x^*(\bullet)\otimes L$. Assume that there exists a universal sheaf $\mathcal{U}$ over $X\times M$. Over $M\times M$ there is a canonical object $\mathcal{E}$, whose ``fiber'' over $(F,F')$ is $\operatorname{Ext}^*(F,F')$. Canonically, it is $R\pi_{23,*}(L\pi_{12}^*\mathcal{U}^\vee\otimes L\pi_{23}^*\mathcal{U})$. When $X$ is an abelian surface, $\operatorname{Ext}^i(F,F')$ vanishes, whenever $i\neq 1$ and $F\not\cong F'$, so that away from the diagonal $\mathcal{E}$ is a locally free sheaf (sitting in degree $1$). In the paper [21] the Weil classes on $X\times\hat{X}$ were constructed via the $\kappa$-class of the pullback of $\mathcal{E}$ to $X\times \hat{X}$ via the morphism \begin{eqnarray*} \iota_{F_1,F_2}:X\times\hat{X}&\rightarrow &\{F_1\}\times M\subset M\times M \\ (x,L)&\mapsto&(F_1,\tau^*_x(F_2)\otimes L). \end{eqnarray*} The pullback $\iota_{F_1,F_2}^*\mathcal{E}$ is shown to be a shift of $\Phi(F_2\boxtimes F_1^\vee)$ in Lemma 6.2.1 in [22] answering the above question.



6. State without proof Lemma 6.1.1 relating the cohomological isomorphism induced by Orlov's equivalence $\Phi$ to Chevalley's isomorphism $\tilde{\varphi}$.



7. State Prop. 4.2.5.3 and 4.2.5.4 in [12] about the homomorphism \[ \gamma_X:\operatorname{Aut}(D^b(X))\rightarrow \operatorname{Aut}(X\times\hat{X}) \] and its kernel.



8. State Prop. 4.3.7 and Lemma 4.3.9 in [12] and relate it to the short exact sequence (3) from Lecture 7.



9. Mention Equation (6.1.9) in [22] describing the difference between the homomorphism $\gamma_X$ and the homomorphism \[ \operatorname{Aut}(D^b(X))\rightarrow \operatorname{Aut}(D^b(X\times X))\rightarrow \operatorname{Aut}(D^b(X\times\hat{X})). \] (composition of the "diagonal" embedding with conjugation by $\Phi$).



10. Present the $\operatorname{Spin}(V)$-equivariant homomorphism \begin{equation} \tag{5} \tilde{\phi}:H^*(X\times X,\mathbb{Z})=S\otimes_\mathbb{Z} S\rightarrow \wedge^*V_\mathbb{Q}=H^*(X\times\hat{X},\mathbb{Q}) \end{equation} in Equation (1.3.2) in Section 1.3 in the introduction of [22] (without the proof of Prop. 1.3.1 in [22] but with the proof of Cor. 1.3.2 in [22]).



11. Point out that the $\operatorname{Spin}_{Hdg}(V)$-action on $H^*(X\times X,\mathbb{Z})$ is induced by the action of derived equivalences and it does not preserve the grading. It is conjugated by $\tilde{\phi}$ to a $\operatorname{Spin}_{Hdg}(V)$-action on $H^*(X\times\hat{X},\mathbb{Z})$ induced by automorphisms of $X\times \hat{X}$, which preserve the grading. (Although $\tilde{\phi}$ is not integral, it conjugates elements of $\operatorname{Spin}(V)$ to integral graded automorphisms of the ring $H^*(X\times\hat{X},\mathbb{Z})$.) Automorphisms act on cohomology via monodromy operators, and in [12] this conjugation by the cohomological isomorphism induced by (essentially) $\Phi$ is interpreted as a version of homological mirror symmetry, relating equivalences of derived categories on the complex "side" to (symplectic) monodromy operators on its mirror.

11. Hodge Weil classes on $X\times\hat{X}$ from tensor squares of pure spinors

1. State III.3.2 in [8] relating the top exterior power $\wedge^{2n}W\subset \wedge^{2n}V_\mathbb{C}$ of a maximal isotropic subspace $W\subset V_\mathbb{C}$ to the image of the tensor square $\ell_W\otimes\ell_W\subset S_\mathbb{C}\otimes S_\mathbb{C}$ of the line $\ell_W$ spanned by pure spinors corresponding to $W$.



2. Prove part (1) of Prop. 6.4.1 in [22] using the following simplified argument. Set $\phi':=\phi\circ (id\otimes\tau)$, where $\phi:H^*(X\times X,\mathbb{Z})\rightarrow H^*(X\times\hat{X},\mathbb{Z})$ is the isomorphism induced by Orlov's derived equivalence and $\tau$ is the dualization involution given in Eq. (1.2.3) in [22] acting on $H^i(X)$ by multiplication by $(-1)^{i(i-1)/2}$. Let $\ell_i\subset H^{ev}(X,K)$ be the line of pure spinors corresponding to $W_i$, $i=1,2$. Note that $\ell_1\oplus\ell_2=P_K$ is defined over $\mathbb{Q}$. The lines $\ell_i^2:=\ell_i\otimes\ell_i$ are in $H^*(X\times X,K)$ and their direct sum is defined over $\mathbb{Q}$. Prop. 6.4.1(1) in [22] states that $\phi'(\ell_1^2\oplus\ell_2^2)$ is contained in $\oplus_{i\geq 2n}H^i(X\times\hat{X},\mathbb{Q})$ and its projection to $H^{2n}(X\times\hat{X},\mathbb{Q})$ maps it isomorphically onto $HW(X\times\hat{X},\mathbb{Q})$.
   Let $\mathcal{P}$ be the Poincaré line bundle over $X\times\hat{X}$. Set \[ \tilde{\phi}(\bullet):=\exp(-c_1(\mathcal{P})/2)\cup\phi'(\bullet). \] The isomorphism $\tilde{\phi}:H^*(X\times X,\mathbb{Q})\rightarrow H^*(X\times\hat{X},\mathbb{Q})$ is the $\operatorname{Spin}(V)$-equivariant isomorphism of Diagram (1.3.1) in [22] (see Equation (5) in Lecture 10).

   Proof of Prop. 6.4.1(1) in [22]: The $\operatorname{Spin}(V)_P$-invariant subring $H^*(X\times\hat{X},\mathbb{Q})^{\operatorname{Spin}(V)_P}$ decomposes as the direct sum \[ H^*(X\times\hat{X},\mathbb{Q})^{\operatorname{Spin}(V)_P}=\operatorname{span}\{h_P^i\}_{i=0}^{2n}\oplus HW(X\times\hat{X},\eta_P), \] by Lemma 2.2.7 in [22] presented in Lecture 7. The first summand is $\operatorname{Spin}(V)_{\ell_1,\ell_2}$-invariant, and $HW(X\times\hat{X},\eta_P)$ is the direct sum of the two one-dimensional $\operatorname{Spin}(V)_{\ell_1,\ell_2}$-representations $\wedge^{2n}W_i$, with characters $\det_i$, $i=1,2$, by Lemma 2.2.7 in [22].
   The subspace $P\otimes P$ is contained in $H^*(X\times X,\mathbb{Q})^{\operatorname{Spin}(V)_P}$ and decomposes as \[ P\otimes P= [(\ell_2\otimes\ell_1) \oplus (\ell_1\otimes \ell_2)]\oplus [\ell_1^2 \oplus \ell_2^2]. \] Each of the summands $(\ell_1\otimes\ell_2)$ and $(\ell_2\otimes\ell_1)$ is the trivial $\operatorname{Spin}(V)_{\ell_1,\ell_2}$-representation, by III.3.3 in [8]. The summand $\ell_i^2$ in $P\otimes P$ corresponds to the character $\det_i$ of $\operatorname{Spin}(V)_{\ell_1,\ell_2}$, by III.3.2 in [8]. Hence, the isomorphism $\tilde{\phi}$ maps $\ell_i^2$ onto $\wedge^{2n}W_i$. Thus, \[ \phi'(\ell_i^2)=\exp(c_1(\mathcal{P})/2)\cup \wedge^{2n} W_i \] is contained in $\oplus_{i\geq 2n}H^i(X\times\hat{X},\mathbb{Q})$ and projects isomorphically onto $\wedge^{2n} W_i$. $\square$

3. Present the short Example 8.2.2 in [22] that every stable sheaf on an abelian surface is a semiregular secant sheaf.



4. Let $C$ be a nonsingular curve of genus $3$ and let $X=\operatorname{Pic}^0(C)$. Let $AJ:C\rightarrow \operatorname{Pic}^1(C)$ be the Abel-Jacobi morphism. Let $C_i$, $1\leq i\leq d+1$, be generic $d+1$ disjoint translates of the image $AJ(C)$ into $X$. Let $\Theta$ be a translate of the theta divisor from $\operatorname{Pic}^2(C)$ into $X$. Denote by $\Theta$ also the class Poincaré dual to $\Theta$ in $H^{1,1}(X,\mathbb{Z})$. Prove Lemma 8.2.1 in [22] stating that the sheaf \begin{equation} \tag{6} F:=\mathcal{I}_{\cup_{i=1}^{d+1}C_i}(\Theta) \end{equation} (the ideal sheaf tensored with $\mathcal{O}_{X}(\Theta)$) is a $\mathbb{Q}(\sqrt{-d})$-secant sheaf in the secant \[ P:=\operatorname{span}_\mathbb{Q}\left\{1-\frac{d}{2}\Theta^2, \Theta-\frac{d}{6}\Theta^3\right\}. \]
5. State and prove Lemma 8.3.1 in [22] that the unique, up to scalar factor, $\operatorname{Spin}(V)_P$-invariant polarization $h\in H^{1,1}(X\times\hat{X},\mathbb{Z})$ satisfies: $h^n$ and $\kappa_n(\Phi(F\boxtimes F))$ are linearly independent. You will use Prop. 6.4.1 in [22] presented in Lecture 11. Relate to Condition (2c) of the general strategy in Lecture 7; the Condition is stated for $E$ arising from two sheaves $F_1$ and $F_2$ on $X$ and we will use two sheaves, but they will have the same Chern character (see (9)).

12. Semiregular secant sheaves on abelian $3$-folds

Keep the notation of lecture 11. In this lecture we prove that the sheaf $F$ given in (6) in the previous lecture is close to being semiregular, and when the collection $\{C_i\}_{i=1}^{d+1}$ is chosen to be an orbit of a cyclic group $G\subset X$, then the ideal $\mathcal{I}_{\cup _{i=1}^{d+1} C_i}$ is the pullback of a semiregular sheaf over $X/G$.

1. State and prove Lemma 8.3.2 in [22] that the natural homomorphism \[ H^0(TX)^{\oplus (d+1)}\oplus H^1(X,\mathcal{O}_{X})\rightarrow \operatorname{Ext}^1(F,F) \] is an isomorphism.
   
   
2. Review the definition of Hochschild cohomology $HH^i(X)$ and the algebra homomorphism \[ev_F: HH^*(X)\rightarrow \operatorname{Ext}^*(F,F)\] of Eq. (8.3.3) in [22]. Denote its restriction to $HH^2(X)$ by $ob_F$. Briefly review the HKR isomorphism $HH^*(X)\cong HT^*(X)$. Note that $H^*(X,\mathbb{C})$ is an $HT^*(X)$-module.
   
   
3. Let $F$ be a coherent sheaf over an $N$-dimensional compact Kähler manifold $M$. Introduce the commutative diagram (8.3.4) in [22].
   
   
   (7)
   
   
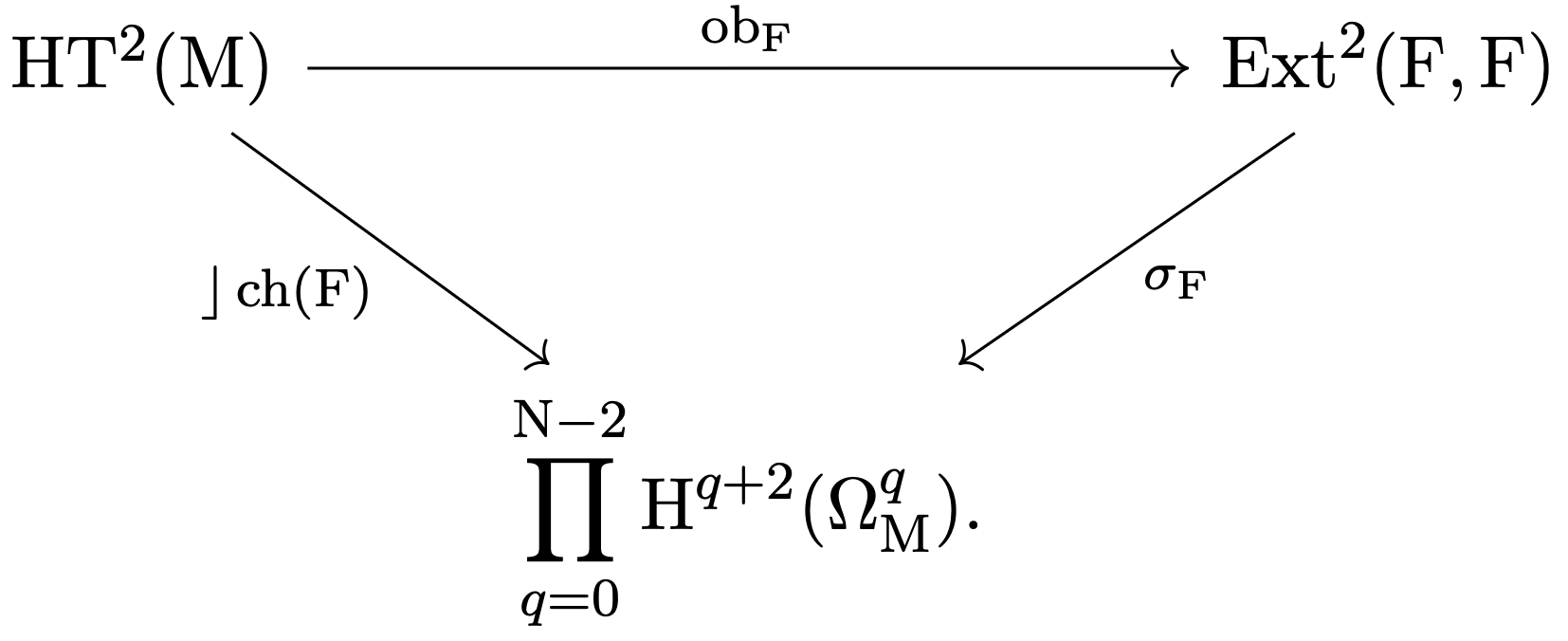
4. State and prove Lemma 8.3.4 in [22]. It states that if $ob_F$ is surjective and the kernels of $ob_F$ is equal to the kernel of $\rfloor ch(F)$, then $F$ is semiregular. Point out that the statement of the Lemma is invariant under equivalences of derived categories; see Rem. 8.3.6 and Lemma 8.3.10 in [22].
   
   
5. State and prove Lemma 8.3.7 in [22] that the ideal sheaf $\mathcal{I}_{C_j}$, of a single translate of the Abel-Jacobi curve in $X$, is semiregular.
   
   
6. State (without proof) a shorter version of Lemma 8.3.8 in [22] that the Yoneda algebra $\operatorname{Ext}^*(F,F)$ of the sheaf $F$, displayed above in (6), is generated by $\operatorname{Ext}^1(F,F)$. Conclude that $ob_F$ is surjective.
   
   
7. State (without proof) Prop. 8.3.9 in [22] that the rank of $ob_F$ is $6$. Point out that when the set $\{C_j\}_{j=1}^{d+1}$ is the orbit of $C_1$ under translations by a subgroup $G\subset X$ of order $d+1$, then the quotient morphism $q:X\rightarrow \bar{X}:=X/G$ maps $C_1$ isomorphically onto a curve $\bar{C}\subset \bar{X}$, the ideal sheaf $\mathcal{I}_{\cup_{i=1}^{d+1}C_i}$ is the pullback of $\mathcal{I}_{\bar{C}}$, and \[ Lq^*:\operatorname{Ext}^*(\mathcal{I}_{\bar{C}},\mathcal{I}_{\bar{C}})\rightarrow \operatorname{Ext}^*(\mathcal{I}_{\cup_{i=1}^{d+1}C_i},\mathcal{I}_{\cup_{i=1}^{d+1}C_i})^G \] is an isomorphism. Furthermore, $\mathcal{I}_{\bar{C}}$ is semiregular and $ob_{\mathcal{I}_{\bar{C}}}$ has rank $6$, essentially by the same proof as that of Lemma 8.3.7 in [22]. In that case Prop. 8.3.9 in [22] follows from the fact that $ob_{\mathcal{I}_{\cup_{i=1}^{d+1}C_i}}$ is $G$-equivariant, the $G$-action on $HT^*(X)$ is trivial, $q^*:HT^*(\bar{X})\rightarrow HT^*(X)$ is an isomorphism, and the diagram
   
   (8)
   
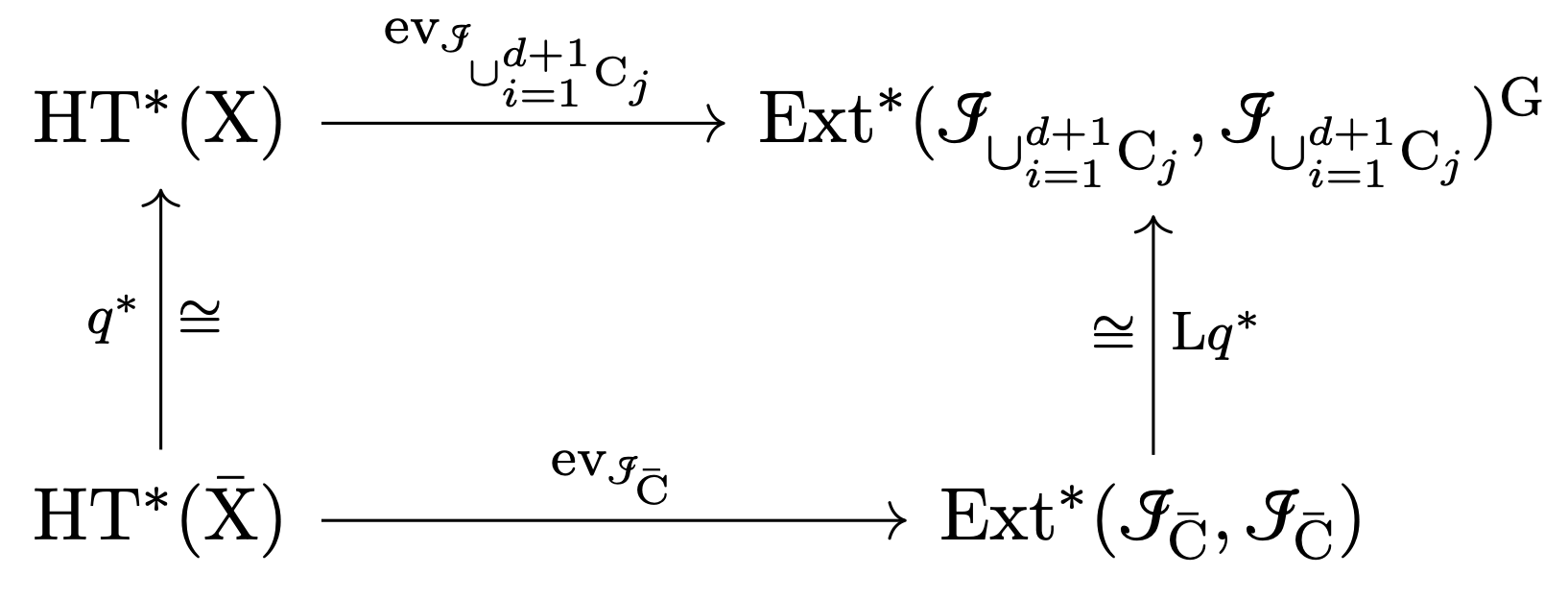
   is commutative.
   
   
8. State and prove Cor. 8.3.12 in [22] that the kernels in $HT^2(X)$ of $ob_F$ and $\rfloor ch(F)$ are equal.

13. An object $E$ of $D^b(X\times \hat{X})$ with a $\operatorname{Spin}(V)_P$-invariant $\kappa(E)$ and a $9$ dimensional $\ker(ob_E)=\ker(\rfloor ch_E)$

We have seen in Lecture 10 how to construct an object $E$ in $D^b(X\times\hat{X})$ with a $\operatorname{Spin}(V)_P$-invariant $\kappa(E)$ from two secant sheaves $F_1$ and $F_2$ on $X$. In lecture 12 we found an equivariantly semiregular secant sheaf $F$. In this lecture we construct an equivariantly semiregular object $\mathcal{G}$ on $X\times\hat{X}$ with a $\operatorname{Spin}(V)_P$-invariant $\kappa(E)$ from two equivariantly semiregular secant sheaves $F_1$ and $F_2$ on $X$. Denote by $F_1\boxtimes F_2$ be the object $\pi_1^*F_1\stackrel{L}{\otimes}\pi_2^* F_2$ in $D^b(X\times X)$. Let $F_1$ and $F_2$ be objects in $D^b(X)$ with $ch(F_i)\in P$ (so secant objects), such that $\ker(\rfloor ch(F_i))=\ker(ob_{F_i})$, for $i=1,2$. Assume, furthermore, that $ev_{F_i}:HT^1(X)\rightarrow \operatorname{Ext}^1(F_i,F_i)$ is injective. For example, $F_1$ could be the sheaf (6) and $F_2$ could be its analogue $\mathcal{I}_{\cup_{i=1}^{d+1}\Sigma_i}(\Theta)$, where $\Sigma=-AJ(C)\subset \operatorname{Pic}(C)^{-1}$ and $\Sigma_j$, $1\leq j\leq d+1$, is a generic collection of disjoint translates of $\Sigma$ into $X$. Note that the classes $[C_i]$ and $[\Sigma_j]$ in $H^6(X,\mathbb{Z})$ are equal, since multiplication by $-1$ acts trivially on $H^{ev}(X,\mathbb{Z})$. Hence, \begin{equation} \tag{9} ch(F_1)=ch(F_2) \end{equation} in this case.

1. State and prove the equation (8.4.3) in [22] \[ \ker(ob_{F_1\boxtimes F_2})=\left[\pi_1^*\ker(ob_{F_1})\otimes \pi_2^*H^0(\mathcal{O}_{X})\right] \ \oplus \ \left[\pi_1^*H^0(\mathcal{O}_{X})\otimes \pi_2^*\ker(ob_{F_2})\right]. \]
   
   
2. Set $E:=\Phi(F_1\boxtimes F_2)$, where $\Phi:D^b(X\times X)\rightarrow D^b(X\times\hat{X})$ is Orlov's equivalence given in (4). State and prove Lemma 8.4.1 in [22] about the equality \[ \ker(ob_E)=\ker(\rfloor ch(E)) \] of subspaces of $HT^2(X\times\hat{X})$.
   
   
3. Define the isomorphism $\Phi^{HT}:HT(X\times X)\rightarrow HT(X\times\hat{X})$ induced by Orlov's equivalence $\Phi$ and the operator $(\bullet)^*: HT^*(X)\rightarrow HT^*(X)$ from Sec. 8.5 of [22]. State, without proof, Cor. 8.5.2 in [22] relating
   1. the $9$-dimensional space $\ker(ob_{F_1})$, of generalized first order deformations of the pair $(X,F_1)$, to
      
      
   2. the $9$-dimensional subspace $\ker(ob_E)$ of $H^1(T[X\times\hat{X}])\oplus H^2(\mathcal{O}_{X\times\hat{X}})$ of commutative and gerby deformations of the pair $(X\times\hat{X},E)$.
   The semiregularity theorem (generalized for twisted sheaves) interprets the latter subspace as the tangent space to the $9$-dimensional moduli space of polarized abelian sixfolds of Weil type deformation equivalent to $(X\times\hat{X},\eta_P,h_P)$. So, at least to first order, these abelian sixfolds of Weil type are a geometric incarnation of the generalized (including commutative, non-commutative, and gerby) deformations of $X$, along which the object $F_1$ deforms.
   Upcoming work of Bayer-Macrì-Pertucci-Perry-… elaborates on this for the analogous case of abelian surfaces and abelian fourfolds of split Weil type. The latter appear as the identity components of the derived categories of non-commutative deformations of an abelian surface, realized geometrically as equivariant categories of sheaves on a carefully chosen family of $K3$-surfaces admitting a suitable involution of their derived category. See also the related Rem. 8.5.5 in [22].
   
   
4. State Assumption 9.1.1 in [22]. State without proof Lemma 9.1.4 in [22] that the assumption is satisfied for a $G$-equivariant collection $\{C_i\}_{i=1}^{d+1}$ in $X$ of translates of the Abel-Jacobi image. (The proof of Lemma 9.1.4 relies on Lemma 9.1.2 in [22], and the latter involves an argument surprisingly rich with the classical geometry of rank $2$ vector bundles with trivial determinant on curves and their relation to divisors in the linear system $2\Theta$ on the Jacobian and, in genus $3$, the Coble quartic.)
   
   
5. State Assumption 9.2.1 in [22].
   
   
6. In Section 9 of [22] there is a change of notation and $F_1$ denotes $F_1^\vee$ in Sec. 8 of [22]. In order to avoid confusion, we will use the notation $K_1:=F_1^\vee$ and $K_2=F_2$, where $F_i$ are as above and as in Sec. 8 of [22]. State (without proof) Prop. 9.2.2 in [22] replacing the notation $F_i$ by $K_i$.
   
   
7. State Lemma 9.2.4 in [22]. Include only Steps 0 and 1 of the proof so that we get the flavor of the proof.

14. A $[\mathbb{Z}/(d+1)\mathbb{Z}]^2$-equivariant sheaf over $X\times \hat{X}$

The first part is a continuation of Lecture 13.

1. See the comment in the previous lecture plan about the change of notation in Sec. 9 of [22].
   
   
2. Present the strategy of the proof of Prop. 9.2.2 in [22] assuming the vanishing criteria (i) and (ii) of the cohomologies $H^i(X,K_1\otimes\tau_x^*(K_2)\otimes L)$. The strategy consist of the part of the proof preceeding the proof of part (1) of the proposition.
   
   
3. Prove that the sheaf $\mathcal{E}$ in Prop. 9.2.2 of [22] has rank $8d$. This involves only the paragraph containing the short exact sequence (9.2.9) in [22]. Do not include the proof of Lemma 11.0.1 in [22].
   
   
4. Explain that the surfaces $\tilde{\Theta}_{i,j}\subset X\times\hat{X}$ consist of points $(x,L)$, where $C_i$ meets $\tau_{-x}(\Sigma_j)$ and the line bundle $\mathcal{O}_{X}(\Theta+\tau_{-x}(\Theta))\otimes L^{-1}$ restricts to the canonical line bundle of $C_i\cup\tau_{-x}(\Sigma_j).$ This causes the failure of vanishing of cohomologies needed for local freeness of $\mathcal{E}$ at that point. The fact that $\mathcal{E}$ is reflexive is not used in the paper.

The proof of the algebraicity of the Weil classes on abelian sixfolds of Weil type is completed in Section 9.3 of [22]. There are two remaining issues. One technical issue is to show that if a sheaf $E$ is semiregular, then the associated twisted sheaf with trivial determinant line-bundle is semiregular as well. We will not elaborate on this technical issue. Granted this, if we could apply Lemma 8.3.4 in [22] (reviewed in Lecture 12) to prove that the sheaf $\mathcal{E}$ of Prop. 9.2.2 in [22] is semi-regular, then we would be done. However, $ob_\mathcal{E}:HT^2(X\times\hat{X})\rightarrow\operatorname{Ext}^2(\mathcal{E},\mathcal{E})$ is not surjective. In fact, $\dim(\operatorname{Ext}^2(\mathcal{E},\mathcal{E}))$ grows quadratically as a function of $d$ as $d\rightarrow\infty$ (by Lemma 8.3.2 in [22], reviewed in Lecture 12, and Serre's duality), while the dimension of the domain of $ob_\mathcal{E}$ is fixed. The solution is to replace $\mathcal{E}$ with a closely related sheaf, which is equivariant with respect to a group $\bar{G}$ of translations isomorphic to $[\mathbb{Z}/(d+1)\mathbb{Z}]^2$, so that it descends to a sheaf $\bar{\mathcal{E}}$ over $(X\times\hat{X})/\bar{G}$ with a surjective $ob_{\bar{\mathcal{E}}}$. The idea was already employed in Diagram (8) above to simplify a proof, but its application below is essential.

1. Let $G_1$ and $G_2$ be cyclic subgroups of $X$ of order $d+1$, such that $G_1\cap G_2=(0)$. Choose the collections $\{C_i\}_{i=1}^{d+1}$ to be $G_1$-equivariant and the collection $\{\Sigma_i\}_{i=1}^{d+1}$ to be $G_2$-equivariant. State, without proof, Lemma 9.3.1 in [22]. It states that genericity Assumption 9.2.1 in [22] holds in this case.
   
   
2. Set \begin{eqnarray*} E'&:=&\mathcal{I}_{\cup_{i=1}^{d+1}\Sigma_i}\boxtimes\mathcal{I}_{\cup_{i=1}^{d+1}C_i}, \\ \Theta\boxtimes\Theta&:=&\pi_1^*\mathcal{O}_{X}(\Theta)\otimes\pi_2^*\mathcal{O}_{X}(\Theta), \\ \mathcal{G}&:=&\Phi(E'\otimes[\Theta\boxtimes\Theta])[-3], \\ \tilde{\Phi}&:=&\Phi\circ([\Theta\boxtimes\Theta]\otimes(\bullet)): D^b(X\times X)\rightarrow D^b(X\times\hat{X}). \end{eqnarray*} Let $G\subset \operatorname{Aut}(D^b(X\times\hat{X}))$ be the image of $G_2\times G_1\subset\operatorname{Aut}(D^b(X\times X))$ via conjugation by $\tilde{\Phi}$. Note that $E'$ is $G_2\times G_1$-equivariant. Hence $\mathcal{G}$ is $G$-equivariant in the sense of [3]. Do not spend time elaborating on group actions on derived categories $D^b(M)$ more general than those arising from groups of automorphisms of $M$. Although the $G$-action is such, below we very quickly return to the special case of groups of automorphisms of $M=X\times\hat{X}$. State and prove Lemma 9.3.2 in [22] about the equality of the image of $ob_\mathcal{G}:HH^2(X\times\hat{X})\rightarrow \operatorname{Hom}(\mathcal{G},\mathcal{G}[2])$ and $\operatorname{Hom}(\mathcal{G},\mathcal{G}[2])^G$.
   
   
3. State and prove Lemma 9.3.3 in [22]. The group $G_2\times G_1$ is contained in the identity component of $D^b(X\times X)$. Hence, $G$ is contained in the identity component $(X\times\hat{X})\times\operatorname{Pic}^0(X\times\hat{X})$ of $\operatorname{Aut}(D^b(X\times\hat{X}))$. The Lemma states that $G$ projects injectively into the factor $X\times\hat{X}$, acting on $\operatorname{Aut}(D^b(X\times\hat{X}))$ via pushforward by translation automorphisms of $X\times\hat{X}$. We get a subgroup $\bar{G}\subset X\times\hat{X}$ isomorphic to $G_2\times G_1$.
   
   
4. State and prove Lemma 9.3.5 in [22]. It states that when $d$ is even, we can tensor $\mathcal{G}$ by a suitable power $a$ of $D:=\det(\mathcal{G})$, so that $\mathcal{G}\otimes D^a$ is $\bar{G}$-equivariant. Mention the statement of Footnote 25 in [22] that $\mathbb{Q}(\sqrt{4d})=\mathbb{Q}(\sqrt{d})$, so all imaginary quadratic number fields are considered even if we assume that $d$ is even.
   
   
5. Set $Y:=[X\times\hat{X}]/\bar{G}$ and denote the quotient morphism by $q:X\times\hat{X}\rightarrow Y$. Set $\mathcal{E}:=(\mathcal{G}^1)^*$, as in Prop. 9.2.2 of [22]. Then $\mathcal{E}\otimes D^{-a}$ is $\bar{G}$-equivariant and it descents to a coherent sheaf $\bar{\mathcal{E}}$ over $Y$. Construction 7.3.3 in [22] (discussed in Lecture 5) applied to $\bar{\mathcal{E}}$ produces a twisted sheaf $\mathcal{B}$, with respect to a Brauer class $\theta$ in $H^2(Y,\mu_r)$, $r=8d$, with trivial determinant, such that $q^*\mathcal{B}$ is a $q^*\theta$-twisted sheaf related to $\mathcal{E}$ by Construction 7.3.3 in [22]. The sheaf $\mathcal{B}$ is constructed in Lemma 9.3.6 of [22] for odd $d$ as well, but we do not need it.
   
   
6. Conclude, that $ob_{\bar{\mathcal{E}}}$ is surjective, by Lemma 9.3.2 in [22] discussed above. Hence, $\bar{\mathcal{E}}$ is semi-regular, by Lemma 8.3.4 in [22].

15. The $CM$-fields case

We review the more general open problem of the algebraicity of the Weil classes on abelian varieties of Weil type with complex multiplication by a CM-field. A CM-field is a totally complex quadratic extension $K$ of a totally real number field $F$. The case $F=\mathbb{Q}$ is the case of imaginary quadratic number fields. The basic definitions of the Weil classes are in Sec. 4 of \cite{deligne-milne}. A more detailed exposition is found in Sec. 11.5.4, 11.5.5 of [9]. The Weil classes appear in $H^d(A,\mathbb{Q})$, where $d=\dim_K(H^1(A,\mathbb{Q}))$, and are no longer in the middle dimension, when $[K:\mathbb{Q}]>2$.

The general strategy for proving the algebraicity of the Weil classes, outlined in Lecture 7, is extended to the CM-field case in [23] (see also [24] for a concise summary). We start with an abelian variety $X$ with real multiplication $\hat{\eta}:F\rightarrow \operatorname{End}_\mathbb{Q}(X)$ and construct complex multiplication $\eta:K\rightarrow \operatorname{End}_\mathbb{Q}(X\times\hat{X})$ in a manner analogous to the one in Lecture 8. The secants in $\mathbb{P}(H^{ev}(X,\mathbb{C}))$ are no longer lines, but rather linear subspaces of dimension $2^{[F:\mathbb{Q}]}-1$. The challenge is to find semiregular secant sheaves with Chern characters in these secant spaces.

In a recent paper Milne points out that if the Weil classes are proven to be algebraic (over complex algebraic varieties), important conjectures in arithmetic algebraic geometry would follow, and a theory of abelian motives over fields of finite characteristic would be available; see Footnote 3 in [25] (the footnote does not appear in the current archive version of this paper arXiv:2508.09972.v2). The importance of the Weil classes stems from a result of André that proves the Hodge conjecture for abelian varieties of CM-type (whose special Mumford-Tate group is a torus, different from Weil-type) assuming the algebraicity of the Weil classes on abelian varieties of split Weil-type [1] (surveyed in Sec. 11.5.6 of [9]). Abelian varieties of CM-type are rigid, corresponding to special points in Shimura varieties. Reduction mod $p$ relates them to abelian varieties over finite fields.

1. Define abelian varieties of CM-type following Sec. 11.5.1 in [9].
   
   
2. Present the construction of the Weil classes on an abelian variety of split Weil type with complex multiplication by a CM-field, following Sec. 11.5.4 and 11.5.5 in [9].
   
   
3. Present the proof of André's theorem following Sec. 11.5.6 in [9].