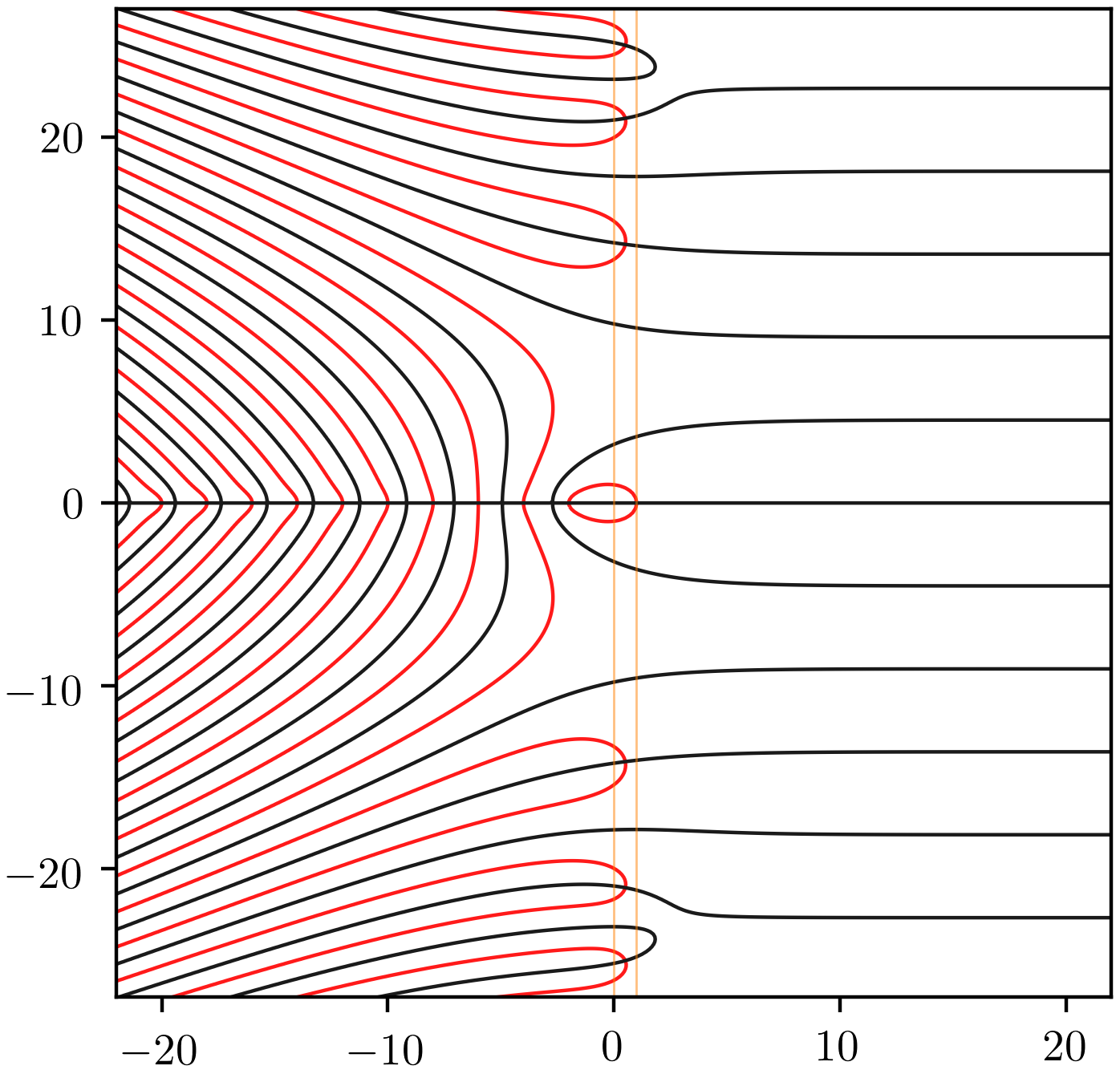
Les fonctions méromorphes aux rayons X¶
Le graphe « x-ray » d’une fonction méromorphe \(f:\C\to\C\) est obtenu en traçant les deux courbes
\(\im(f)=0\), en noir ; c’est-à-dire l’endroit où \(f(z)\) est réel.
\(\re(f) = 0\), en rouge, là où \(f(z)\) est imaginaire pur.
En particulier, les endroits où deux courbes s’intersectent sont des zéros (ou des pôles) de la fonction \(f\).
Quelques exemples de graphes « x-ray »:
l’identité
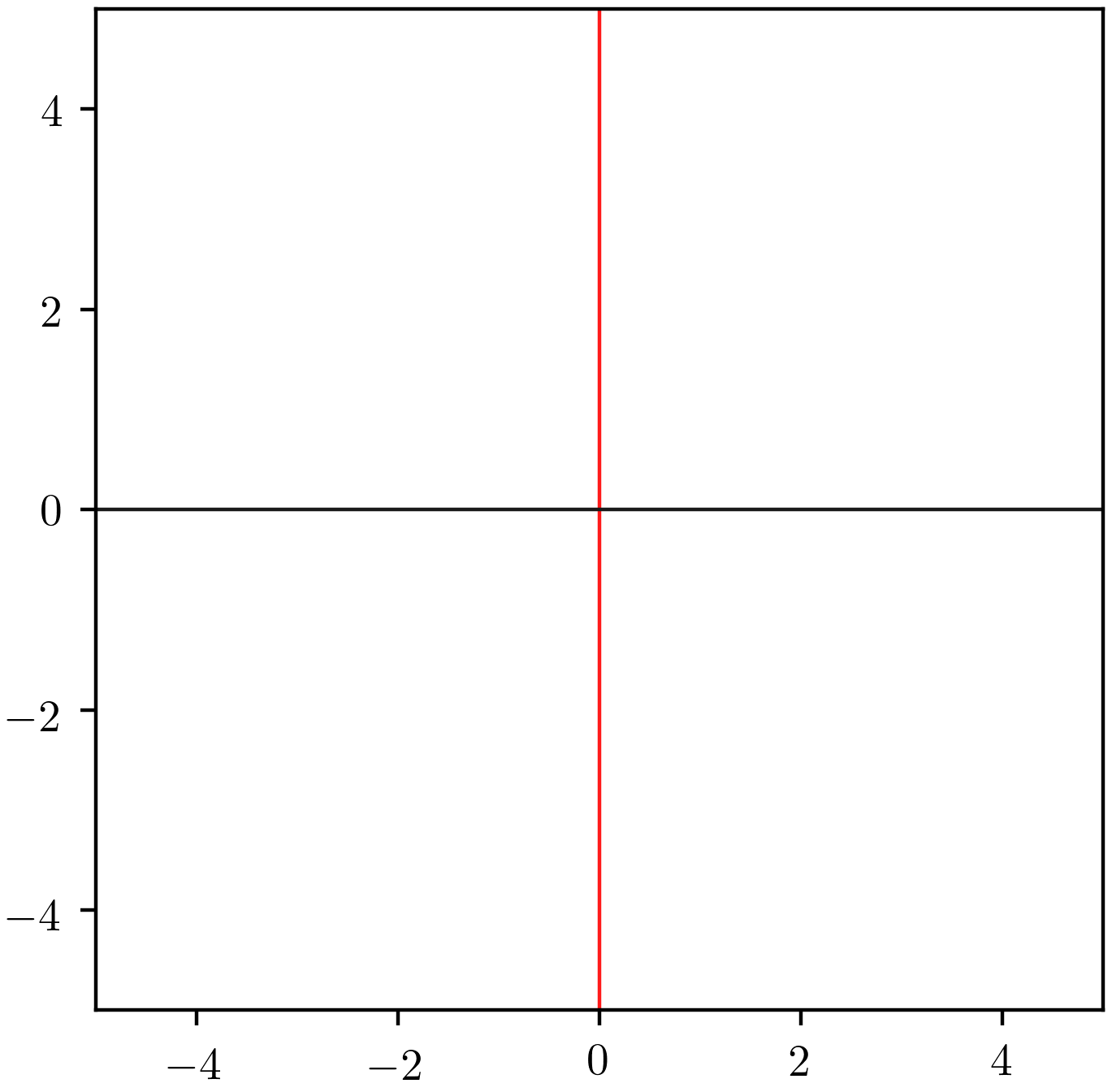
la fonction exponentielle
la fonction sinus
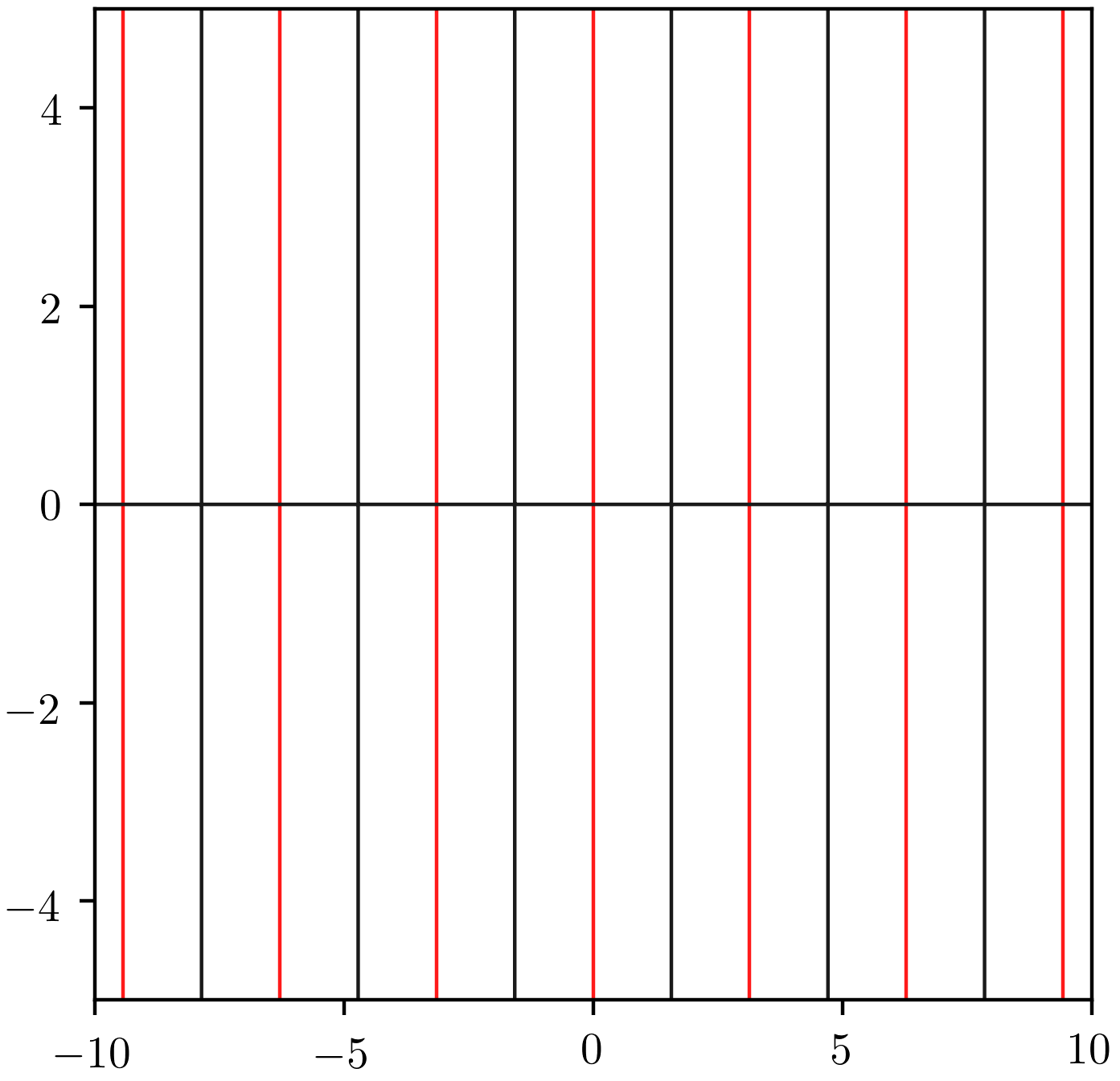
un polynôme (ici \(-9x^6 - 15x^4 + 9x^3 + 3x^2 - 2x + 5\))
On remarque les zéros là où les courbes s’intersectent.
Les intersections de courbes de même couleur signalent des zéros de la dérivée.
la fonction gamma \(\Gamma_\R\)
la fonction zeta
Quelques commentaires :
sur les zéros
on voit les zéros triviaux sur l’axe réel
et les zéros non triviaux sur la droite critique
sur le comportement à droite
par de courbe rouge, en effet par convergence uniforme la partie réelle ne peut pas s’annuler
on obtient des droites régulières, en effet \(\im(\zeta(x+it))=\sum_{n\geq 2}\frac{\sin(t\log n)}{n^x}\approx \frac{\sin(t\log 2)}{2^x}\).
sur les courbes noires issues de droite
\(\zeta(s)\to 1\) uniformément, et la fonction est monotone. Donc soit on vient de \(-\infty\) et la courbe passe par un zéro, soit on vient de \(+\infty\) et il n’y en a pas.