What is Fission?
We use the word "fission" to denote the breaking of structure group of a connection on a bundle on a Riemann surface. If the structure group breaks from a Lie group $G$ into a product $H=H_1\times H_2$ of two Lie groups then the surface can break up, or "fission", into two pieces of surface that do not interact, one with a $H_1$ connection and one with a $H_2$ connection.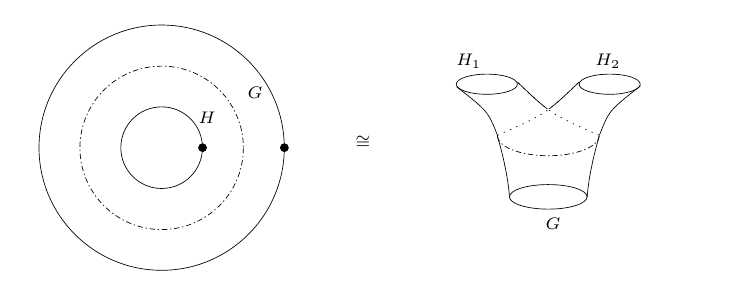
This term was first used in this manner in [B09], but the first examples of fission spaces appeared in [B02], as a way to package the explicit presentations of wild character varieties due to Birkhoff/Jimbo-Miwa-Ueno [Bi13, JMU] in terms of quasi-Hamiltonian geometry, as well as their generalisation to other structure groups beyond $\GL_n(\IC)$. As discussed there, any irregular singular meromorphic connection leads to such a breaking of structure group, when the connection is described topologically. The topological symplectic structure on the wild character variety is induced from the quasi-Hamiltonian structures on the fission spaces. This was the main motivation for this TQFT approach to wild character varieties, gluing pieces of surface. See this video for a recent introduction/summary of these ideas, or maybe this minicourse.
This leads to several related mathematical objects:
A basic example of the type of changes of structure group that occur is the breaking to the block diagonal subgroup $H=\GL_a(\IC)\times\GL_b(\IC)$ in the group $G=\GL_{a+b}(\IC)$ for any integers $a,b$: $$\GL_a(\IC)\times\GL_b(\IC)\subset \GL_{a+b}(\IC).$$ For example if we consider three such subgroups then one gets pictures that look as follows (taken from [B09]):
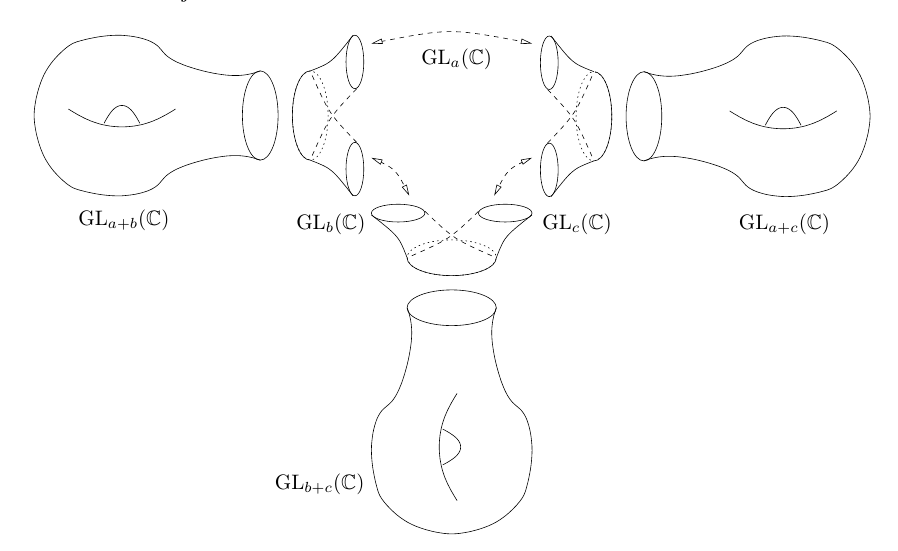
This picture determines a symplectic variety, an example of a fission variety.
Beware that this notion of fission is not the inverse of "fusion": fusion involves gluing two boundary circles into two holes of a three-holed sphere, and does not involve changing the structure group.
Fission spaces $\cA,\cB$
The fission spaces are a class of algebraic quasi-Hamiltonian spaces. They enable the breaking of structure group from a group $G$ to a subgroup $H\subset G$.Geometrically the fission spaces $\cA$ are the wild representation varieties for meromorphic connections with just one level on a complex disk. The reduced fission spaces $\cB$ are the wild representation varieties for meromorphic connections with just one pole on the Riemann sphere. They arise by capping off the $G$ boundary of the fission spaces: $\cB=\cA\spq{} G.$
The simplest example is $$\cA={_G\!\,\cA_T}\cong G\times U_+\times U_-\times T$$ where $G$ is a complex reductive group, $H=T\subset G$ is a maximal torus, and $U_\pm\subset G$ are the full unipotent subgroups inside a pair of opposite Borel subgroups $B_\pm\subset G$. It has dimension $2\dim(G)$. This example appeared in [B02] p.6 (denoted $\wt \cC/L$ there; they are closely related to the extended conjugacy classes $\wt \cC$ in [B99,B01]). It is equipped with the structure of quasi-Hamiltonian space and comes equipped with a group-valued moment map $$\mu=(\mu_G,\mu_T):\cA\to G\times T; \qquad (C,S_1,S_2,h)\mapsto (ChS_2S_1C^{-1}, h^{-1}).$$ In brief this means we can do fusion and reduction to construct many more quasi-Hamiltonian/Poisson/symplectic spaces. More generally [B02] defined the higher fission spaces $$\cA={_G\!\,\cA^k_T}\cong G\times(U_+\times U_-)^k\times T$$ for any integer $k$, and showed they also are quasi-Hamiltonian. These example all give a mechanism to break the structure group from $G$ to the maximal torus $T$.
Amongst these the simplest example (described in many ways in [B15a]) is to take $G=\GL_2(\IC)$ so the fission space is : $$\cA={_G\!\,\cA_T^{k}}\cong G\times (U_+\times U_-)^k\times T$$ $$ \text{where }\quad U_+ = \bmx 1 & * \\ 0 & 1 \emx,\qquad U_- = \bmx 1 & 0 \\ * & 1 \emx,\qquad H = T= \bmx * & 0 \\ 0 & * \emx\ \subset G.$$ As explained in [B15a] the corresponding reduced fission space $\cB=\cA\spq G$ can be described as $$\cB\cong \{ \bS\in (U_+\times U_-)^k \st S_{2k}\cdots S_2S_1\in T\}$$ where $S_{odd}\in U_+, S_{even}\in U_-$, or as the open subset $$\cB\cong \{ x\in \IC^{n} \st (x_1,\ldots,x_{n})\neq 0 \}$$ where $n=2k-2$ and $(x_1,\ldots,x_{n})$ is the degree $n$ Euler continuant polynomial.
More generally [B09,B14] constructed the higher fission spaces $$\cA={_G\!\,\cA^k_H}\cong G\times(U_+\times U_-)^k\times H$$ for any integer $k$, where now $H\subset G$ is a Levi subgroup of any parabolic $P_+\subset G$ and $U_\pm$ are the unipotent radicals of $P_\pm$ where $P_-$ is the opposite parabolic to $P_+$, so that $H=P_+\cap P_-$.
By gluing such fission spaces end to end (for a decreasing sequence of Levi subgroups $H_i$) the paper [B14] constructed all the (untwisted) wild character varieties as algebraic Poisson varieties.
More generally [BY15] constructed the twisted fission spaces, and used them to complete the construction of the wild character varieties as algebraic Poisson varieties (and to construct their analogues where the group $G$ is allowed to "twist" over the interior of the Riemann surface). A simple twisted example is the fission space: $$\cA={_G\!\,\cA_H^{k/2}}\cong G\times U_\pm^{(k)}\times H(\partial)$$ determined by a vector space $V=W\oplus W$ and an odd integer $k\ge 1$, where $G:=\GL(V)$ (so elements of $G$ can be written as $2\times2$ block matrices), and we consider the following subgroups of $G$: $$ U_+ = \bmx 1 & * \\ 0 & 1 \emx,\qquad U_- = \bmx 1 & 0 \\ * & 1 \emx,\qquad H = \bmx * & 0 \\ 0 & * \emx\ \subset G $$ and the subset $H(\partial) = \bsmx 0 & * \\ * & 0 \esmx\subset G$, which is a twist of $H$, and $$U_\pm^{(k)} = U_+\times U_- \times U_+\times\cdots$$ where there are $k$ groups in total on the right.
These examples are determined by irregular classes with Stokes diagrams of the form:
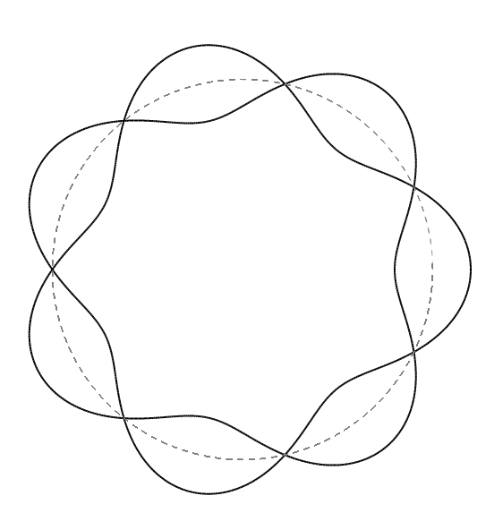
where there are $k$ crossings (see the explanations in [BY15, B21] and beneath the app here. In particular [B21] summarises how the Stokes diagram determines the Stokes groups $U_\pm$).
Fission varieties
The "fission varieties" are the class of holomorphic symplectic/Poisson varieties that appear by fusing together the fission spaces and then reducing. See [B14] §3.2 and the examples of gluing data in [B09] (as well as the more general twisted cases stemming from [BY15]).A key point is that the fission varieties are much more general than the wild character varieties (in essence the fission spaces were introduced as building blocks to give a clean algebraic construction of the wild character varieties, and then it was clear that many other varieties can also be constructed).
The multiplicative quiver varieties, and their colourful generalisations [B15], are examples of fission varieties, and most of them are not isomorphic to wild character varieties.
Fission trees
The fission trees are trees indicating the sequential way in which the structure group is broken at the boundary, determined by an irregular type or irregular class. They were first defined in [B08] Appendix C in the untwisted general linear case, and recently have been generalised in several ways [DRT22, DR22, BDR22]. See the slide below for an illustration of this.Fission graphs
The motivation for considering the fission trees in [B08] Appendix C was to define the graphs (or "doubled quivers") that occur in nonabelian Hodge theory (sometimes called the "fission graphs", or "nonabelian Hodge graphs").The fission graphs appear in the quiver modularity conjecture of [B08], that the corresponding Nakajima quiver varieties appear as additive moduli spaces in wild nonabelian Hodge theory. It was proved in general by Hiroe-Yamakawa [HY14].
See e.g. p.103 of these slides (from this talk) for an illustration of this:
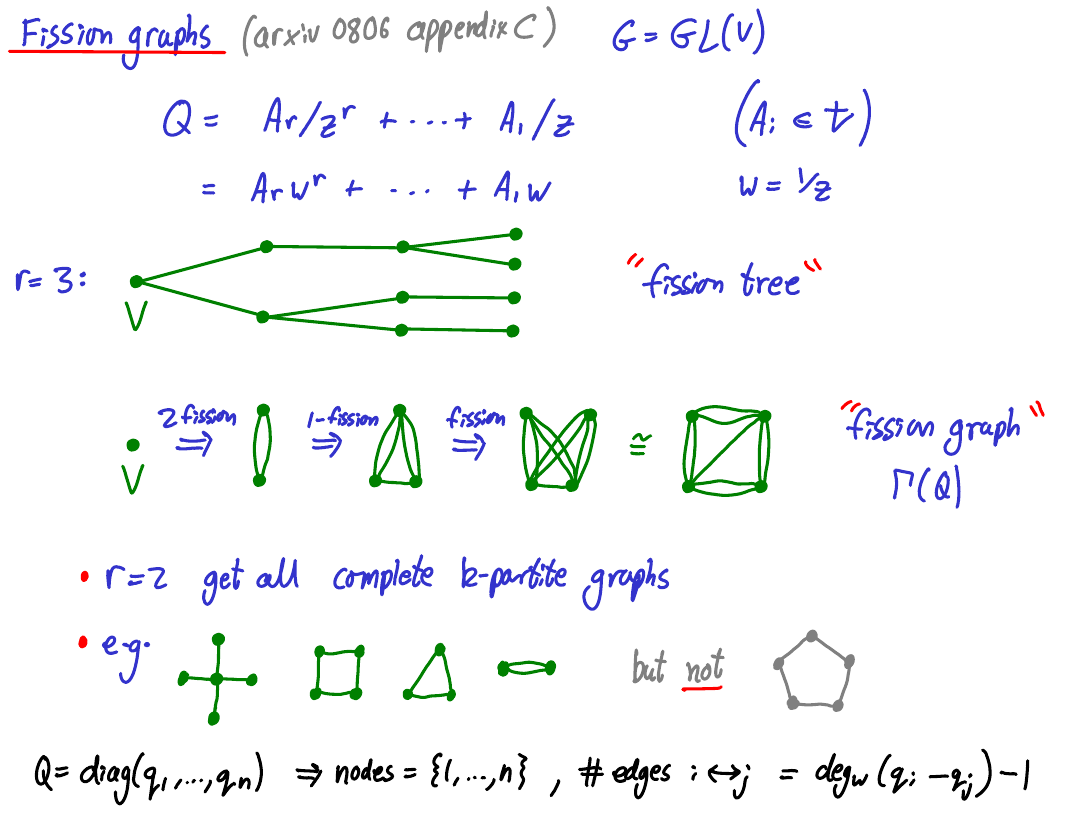
The fission graphs were generalised to the twisted case to yield the nonabelian Hodge diagrams of [BY20], and their scope was subsequently generalised in [D21]
Fission operation on graphs
The method of constructing the fission graphs in [B08] (see the slide above) involved various operation on graphs, called fission (= 0-fission), 1-fission, 2-fission etc. The operation of 0-fission was also called "splaying" in [B08] p.26:
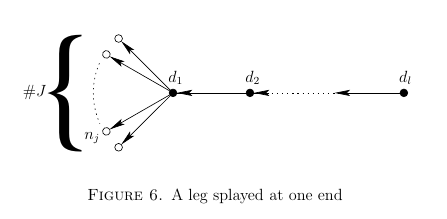
Fission surfaces
The surfaces obtained by performing fission at a boundary circle, as in the following picture (from [B21]):
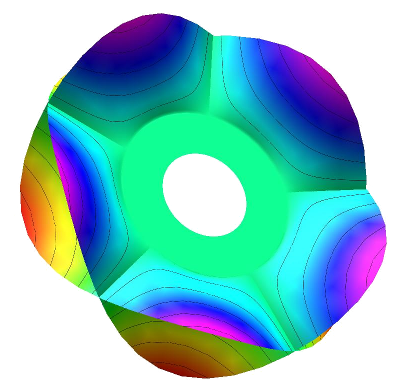
The paper [B21] §8 describes how one can think of Stokes local systems in terms of (generalised) local systems on fission surfaces (gluing the graded local system to the interior local system), in the general linear case.
Fission algebras
The term "fission algebra" was used in [B15] §12 for the algebras that generalise the deformed multiplicative preprojective algebras of [CBS06]. They are related to the colourful multiplicative quiver varieties of [B15] in the same way that the usual deformed multiplicative preprojective algebras are related to the usual multiplicative quiver varieties.See also the "deeper" example of a fission algebra presented in [B15a] Rmk 17.
Fission conjecture
The conjecture in [B09] that the fission varieties are hyperkahler.References
[Bi13] G.D. Birkhoff, The generalized Riemann problem for linear differential equations and allied problems for linear difference and q-difference equations, Proc. Amer. Acad. Arts and Sci., 49, 1913 531-205.[B99] P.P. Boalch, Symplectic geometry and isomonodromic deformations, D.Phil. Thesis, Oxford University, (tel-02357236), 1999.
[B01] P.P. Boalch, Symplectic manifolds and isomonodromic deformations, Adv. in Math. 163 (2001), 137–205.
[B02] P.P. Boalch, Quasi-Hamiltonian geometry of meromorphic connections, math.DG/0203161. (Published in Duke 2007.)
[B08] P.P. Boalch, Irregular connections and Kac–Moody root systems, arXiv:0806.1050, 2008.
[B09] P.P. Boalch, Through the analytic halo: Fission via irregular singularities, Ann. Inst. Fourier (Grenoble) 59 (2009), no. 7, 2669–2684, Volume in honour of B. Malgrange.
[B14] P.P. Boalch, Geometry and braiding of Stokes data; Fission and wild character varieties, Annals of Math. 179 (2014), 301–365.
[B15a] P.P. Boalch, Wild character varieties, points on the Riemann sphere and Calabi's examples, Representation theory, special functions and Painlevé equations—RIMS 2015, Adv. Stud. Pure Math., vol. 76, Math. Soc. Japan, Tokyo, 2018, pp. 67–94.
[B15] P.P. Boalch, Global Weyl groups and a new theory of multiplicative quiver varieties, Geometry and Topology 19 (2015), 3467–3536.
[B21] P.P. Boalch, Topology of the Stokes phenomenon, Proc. Symp. Pure Math. 103 (2021) 55–100
[BDR22] P.P. Boalch, J. Douçot and G. Rembado, Twisted local wild mapping class groups: configuration spaces, fission trees and complex braids
[BY15] P.P. Boalch and D. Yamakawa, Twisted wild character varieties, arXiv:1512.08091, 2015.
[BY20] P.P. Boalch, Diagrams for nonabelian Hodge spaces on the affine line, C. R. Math. Acad. Sci. Paris 358 (2020), no. 1, 59–65.
[CBS06] W. Crawley-Boevey and P. Shaw, Multiplicative preprojective algebras, middle convolution and the Deligne–Simpson problem, Adv. Math. 201 (2006) 180–208
[D20] J. Douçot, Diagrams and irregular connections on the Riemann sphere, arXiv:2107.02516 (2021)
[DRT22] J. Douçot, G. Rembado, and M. Tamiozzo, Local wild mapping class groups and cabled braids, arXiv:2204.08188 (2022).
[DR22] J. Douçot and G. Rembado, Topology of irregular isomonodromy times on a fixed pointed curve, arXiv:2208.02575 (2022).
[HY14] K. Hiroe and D. Yamakawa, Moduli spaces of meromorphic connections and quiver varieties, Adv. Math. 266 (2014), 120–151, arXiv:1305.4092.
[JMU] M. Jimbo, T. Miwa, and K. Ueno, Monodromy preserving deformations of linear differential equations with rational coefficients I, Physica 2D (1981), 306–352.