Distance prescrite, codes BCH¶

Polynôme générateur et racines¶

On suppose que $n$ est premier à $q$, et on note $\alpha$ une racine $n$-ième primitive de l’unité dans une extension de $\F_q$.

Si vous suivez...

Soit $\alpha = x\mod x^3+x+1$ sur $\F_2$. Quel est l’ordre de $\alpha$ ?

2
8
7
4

Si vous suivez...

Pour $n=8$ et $q=3$, un choix possible de $\alpha$ est

$5$
$x+1\mod x^2+1$
$i$
$x\mod x^2-x-1$

Alors les racines de $x^n-1$ sont les puissances de $\alpha$, donc les racines du polynôme générateur $g(x)$ sont aussi des puissances de $\alpha$.

On a donc une dernière manière de décrire un code cyclique : par les racines $\alpha^k$ de $g(x)$, c’est-à-dire par l’ensemble $I_g=\set{k\in\Z/n\Z, g(\alpha^k)=0}$.

Si vous suivez...

On pose $\alpha = x\mod x^3+x+1$ sur $\F_2$. Quelles sont les racines de $x^3+x+1$ ?

$\alpha$, $\alpha^2$ et $\alpha^4$
$\alpha$, $1/\alpha$ et $\alpha^4$
$\alpha$, $\alpha^2$ et $\alpha^3$

Si vous suivez...

Avec la même valeur $\alpha = x\mod x^3+x+1$ sur $\F_2$, quelles sont les racines de $x^3+x^2+1$ ?

$\alpha^3$, $\alpha^5$ et $\alpha^6$
$\alpha^3$, $\alpha^5$ et $\alpha^7$
$\alpha^2$, $\alpha^4$ et $\alpha^6$
$\alpha^{-1}$, $\alpha^{-2}$ et $\alpha^{-4}$

Cet ensemble n’est pas quelconque : il est stable par l’action du Frobenius.

Lemme

Soit $g(x)\in\F_q[x]$. Alors $g(\alpha^k)=0\Rightarrow g(\alpha^{qk})=0$.

En particulier, $I_g$ est stable par la multiplication par $q$.

La réciproque est vraie (un polynôme fixé par le Frobenius est à coefficient dans $\F_q$).

Lemme

Soit $I\subset\Z/n\Z$ une partie stable par multiplication par $q$, alors $g(x)=\prod_{k\in I}(x-\alpha^k)$ est un polynôme à coefficients dans $\F_q$ qui divise $x^n-1$.

On a donc une autre manière de chercher les codes cycliques : déterminer les parties $q$-stables.

Exemple

Les $3$-orbites modulo $8$ et les facteurs de $X^8-1$ associés sont

orbite	polynôme	identification
$\set{0}$	$\Phi_1=X-1$
$\set{1, 3}$	$P(X)$	facteur irréductible de $\Phi_8$
$\set{2, 6}$	$\Phi_4 = X^2+1$	diviseur de $X^4-1$ mais pas de $X^2-1$
$\set{4}$	$\Phi_2 = X+1$	facteur de $X^2-1$ mais pas de $X-1$
$\set{5, 7}$	$Q(X)$	facteur irréductible de $\Phi_8$

L’orbite $\set{4}$ correspond à $\Phi_2=X+1$, et $\set{2, 6}$ à $\Phi_4=X^2+1$.

Les orbites $\set{1, 3}$ et $\set{5, 7}$ correspondent aux deux facteurs irréductibles de $\Phi_8$, soient $X^2-X-1$ et $X^2+X-1$.

Si vous suivez...

Déterminer les 3-orbites de $\Z/11\Z$/

La borne BCH¶

Théorème

Soit $C$ un code cyclique de longueur $n$ sur $\F_q$, engendré par le polynôme $g(x)\mid x^n-1$.

Si $g$ s’annule en $r-1$ puissances consécutives de $\alpha$

\[g(\alpha^{a+1})=g(\alpha^{a+2})=\dots g(\alpha^{a+r-1})=0\]

alors $d(C)\geq r$.

Si vous suivez...

On regarde le $[7,4]$ code cyclique binaire engendré par $x^3+x+1$. D’après la borne BCH, sa distance est au moins

1
2
3
4

Démonstration

Soit $\alpha$ la racine $n$-ième permettant d’écrire la correspondance $C-I$. Puisque les racines du générateur sont les $\alpha^i, i\in I$, on a

\[C = \set{m(x), \forall i\in I, m(\alpha^i) = 0}\]

Soit donc $m$ de poids $w(m)\leq r-1$, on écrit $m(x)=\sum_{j=1}^{r-1}m_jx^{d_j}$ et l’on a pour $1\leq i\leq r-1$ des équations

\[\sum_{j=1}^{r-1} m_j \alpha^{d_j(a+i)} = 0.\]

Ainsi, le vecteur $M=(m_j \alpha^{d_j a})$ est dans le noyau de la matrice $(\alpha^{d_j i})$, qui est une matrice de Vandermonde de déterminant non nul puisque les $\alpha^{d_j}$ sont deux-à-deux distincts. Ainsi, $M$ est nul et $m(x)$ est le mot nul.

Remarque

Si on ne connaît pas les déterminants de Vandermonde, il s’agit du déterminant de l’application d’évaluation des polynômes de degré $<r$ en les points $\alpha^{d_j}$, qui est bien injective (pas plus de racines que le degré).

Définition

On appelle code BCH de distance prescrite $\delta$ le code engendré par le produit des polynômes minimaux de $\alpha, \alpha^2, \dots \alpha^{\delta-1}$.

Il se peut qu’il ait distance strictement supérieure à $\delta$.

Exemple

Pour $n=7$ et $q=2$, on considère le polynôme $g(x)=x^3+x+1$. En notant $\alpha=x\bmod g\in\F_8$ (qui est une racine $7$-ième de l’unité), $g$ s’annule en $\alpha,\alpha^2$ et $\alpha^4$. Donc d’après la proposition la distance est supérieure à $3$. Comme $g$ est de poids $3$ on a égalité.

On obient un $[7,4,3]$ code : c’est un code de Hamming.

Exemple

On reprend l’exemple sur les facteurs de $X^8-1$ modulo $3$.

Notons $P(X)=X^2-X-1$ et prenons pour $\alpha$ une racine de $P$ ($\alpha^3$ est donc l’autre racine, tandis que $\alpha^5$ et $\alpha^7$ sont les racines de $Q(X)=X^2+X-1$).

Alors en prenant ce $\alpha$ pour expliciter la correspondance, la partie $I=\set{1, 3, 2, 6}$ contient 3 éléments consécutifs et correspond au code engendré par $P(X)\Phi_4(X)=(X^2-X-1)(X^2+1)=X^4-X^3-X-1$.

C’est un $[8,4]$-code de distance $d\geq 4$. De plus, le générateur est de poids $4$ donc c’est un $[8,4,4]$-code.

Si vous suivez...

Un $[11,7]$ code cyclique ternaire a une distance au moins ?

[code de Golay $G_{11}$]

Sur $\F_3$, le minimal $P(x)$ d’une racine $11$-ième de l’unité $\alpha$ s’annule aussi en $\alpha^3,\alpha^9, \alpha^{5},\alpha^4$. Il est de degré $5$. Le minimal de $\alpha^{-1}$ est $\tilde P(x)$.

Ainsi $x^{11}-1=(x-1)P(x)\tilde P(x)$, avec $P,Q$ irréductibles de degré $5$. On note $G_{11}=\langle P\rangle$, c’est un code cyclique de distance au moins $4$.

Puisque $P(x)\tilde P(x)=\Phi_{11}(x)$, on obtient le diagramme de codes cycliques suivant.

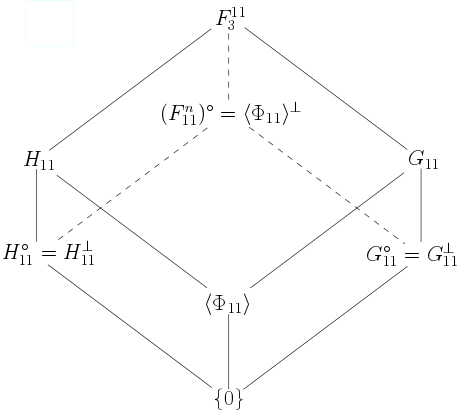
Voir l’exercice pour finir la démonstration que $d(G_{11})=5$.

Code de Reed-Solomon¶

Dans le cas où $k=\F_q$, c’est-à-dire si $\F_q$ contient les racines $n$-ièmes de l’unité, à toute partie $I$ de cardinal $n-k$ correspond un $[n,k,n-k+1]$-code. Il n’est pas nécessaire que les éléments soient consécutifs pour calculer la distance, en effet un polynôme qui s’annule en $n-k$ points On peut aussi caractériser les mots de codes par le fait matrice vérificatrice via les racines de $g$, si l’on se met dans un corps de décomposition de $g$.

Digression: une interprétation harmonique¶

On considère le groupe cyclique $\F_q^\times=\langle\alpha\rangle$ des racines $n$-ièmes de l’unité, pour $n=q-1$.

Pour $X\subset\Z/n\Z$ on note $L(X) = \set{f:X\to\F_q}$ l’espace des fonctions définies sur $X$, autrement dit les mots de longueur $n$ à support dans $X$. $L(\Z/n\Z)=\F_q^n$ est l’espace total.

Alors on a une application de «transformée de Fourier»

\[\begin{aligned} L(\Z/n\Z) &\to L(\Z/n\Z) \\ f &\mapsto \hat f \end{aligned}\]

où l’on pose

\[\hat f(i) = \sum_j \alpha^{ij} f(j).\]

Cette application est bijective, et anti-involutive

\[\widehat{\hat f}(i) = -f(-i)\]

en utilisant

\[\sum_{k}\alpha{(i+j)k} =\begin{cases}n\equiv-1\text{ si }i+j=0\bmod n\\0\text{ sinon}\end{cases}\]

Le code de Goppa obtenu par évaluation des polynômes de degré $<k$ en $1,\dots \alpha^{n-1}$ est alors

\[G_k = \widehat{L(\set{0,\dots k-1})}\]

Le code de Reed-Solomon des mots s’annulant en $1,\dots \alpha^{n-k}$ est l’image réciproque

\[S_k = \set{ f, \hat f\in L(\set{n-k,\dots n})}\]

soit par inversion on a l’égalité

\[S_k = \set{ \hat f, f\in L(\set{0,\dots k})} = G_k\]

Le principe d’incertitude qui affirme qu’on ne peut être localisé à la fois en position et en fréquence se traduit par le fait que $f$ et $\hat f$ ne peuvent tous deux être de petit poids. C’est une situation idéale pour le codage : la transformée de Fourier répartit l’information sur toutes les positions.

Les inégalités d’incertitude générales sont trop faibles, mais on obtient une situation très favorable si l’ordre $n$ est premier (ce qui boucle joliment ce chapitre avec l’arithmétique).

Proposition

Soit $n=2^p-1$ un nombre premier de Mersenne, et $f\in G(\Z/n\Z)$. Alors la somme des poids de $f$ et $\hat f$ est supérieure à $n+1$.

Démonstration

Un théorème de Tao (2005) donne la conclusion sur le support de $f$ et $\hat f$ pour $L(\Z/n\Z)$ quand $n$ est premier. Dans le cadre étudié ici, $n\mid q-1$ s’obtient en particulier pour les nombres premiers de Mersenne.

orbite	polynôme	identification
\(\set{0}\)	\(\Phi_1=X-1\)
\(\set{1, 3}\)	\(P(X)\)	facteur irréductible de \(\Phi_8\)
\(\set{2, 6}\)	\(\Phi_4 = X^2+1\)	diviseur de \(X^4-1\) mais pas de \(X^2-1\)
\(\set{4}\)	\(\Phi_2 = X+1\)	facteur de \(X^2-1\) mais pas de \(X-1\)
\(\set{5, 7}\)	\(Q(X)\)	facteur irréductible de \(\Phi_8\)

Distance prescrite, codes BCH¶

Polynôme générateur et racines¶

La borne BCH¶

Code de Reed-Solomon¶

Digression: une interprétation harmonique¶

Table des matières

Table des matières