Constructions¶
Codes de Hamming¶
Ce sont les codes 1-correcteurs parfaits.
Principe : s’il y a une erreur en position \(i\), le syndrome est (proportionnel à) la i-ième colonne de la matrice vérificatrice. Un code est 1-correcteur si les syndromes sont linéairement distincts, donc si la matrice vérificatrice est formée de colonnes linéairement toutes distinctes. Le code de Hamming s’obtient en prenant les matrices vérificatrices les plus grandes satisfaisant cette propriété, c’est-à-dire formées de tous les vecteurs non nuls à proportionnalité près.
Code de Hamming binaire
Soit \(r\geq 2\), et soit \(V_r\) une matrice \(r\times 2^r-1\) dont les colonnes sont tous les vecteurs non nuls de \(\F_2^r\). On appelle code de Hamming \(H_r(\F_2)\) le code de matrice vérificatrice \(V_r\).
Proposition
\(H_r\) est un \([2^r-1,2^r-r-1,3]\) code linéaire. C’est un code \(1\)-correcteur parfait.
Démonstration
La distance est au moins \(3\) car les colonnes de \(V_r\) sont non proportionelles. En outre, on vérifie l’égalité de Hamming : avec \(n=2^r-1\) et \(k=2^n-r-1\), on a \(\card B(0,1)\card C=(1+n)(2^k)=2^r2^{2^r-r-1}=2^{2^r-1}=2^n\).
Le décodage est particulièrement simple : pour une erreur, le syndrome est une colonne de \(V_r\), qui indique le bit erroné.
Plus généralement, pour tout corps fini \(\F_q\), on construit le code de Hamming \(H_r(\F_q)\) via sa matrice vérificatrice, dont les colonnes forment un ensemble maximal de vecteurs non nuls et deux à deux non colinéaires de \(\F_q^r\). Il y a \(n=\frac{q^r-1}{q-1}\) tels vecteurs, d’où un code \([n,k,3]\), qui est à nouveau parfait.
On a en fait la caractérisation :
Théorème
Soit \(C\) un code linéaire \(1\)-correcteur parfait sur \(\F_q\). Alors \(C\) est un code de Hamming \(H_r\).
Démonstration
En notant \(\card C=q^k\), on pose \(r=n-k\) et on a par égalité de Hamming \(n=\frac{q^{r}-1}{q-1}\). Si le code est \(1\)-correcteur, les colonnes de sa vérificatrices sont non colinéaires, d’où l’équivalence à \(H_r\).
Opérations sur les codes¶
Équivalence¶
En agissant sur les lignes de la matrice génératrice, on ne change pas l’espace que ces lignes engendrent : on garde le même code.
Proposition
Soit \(C\) un \([n,k]\)-code, et \(G\) une matrice génératrice de \(C\). Alors les matrices génératrices de \(C\) sont exactement les matrices de la forme \(AG\), pour \(A\in\Gl_k(\F_q)\).
En revanche, on doit s’interdire de faire des opérations sur les colonnes, ce qui change la base de l’espace \(\F_q^n\) ambiant, et donc la distance de Hamming.
Toutefois, cette distance est préservée si on permute les coordonnées par un élément de \(S_n\). On dira que deux codes sont équivalents s’ils se déduisent l’un de l’autre par une telle permutation des indices.
On a vu que tout code est équivalent à un code sous forme systématique.
Codes étendu, raccourci, sous-code pair¶
L’image d’un code par une application linéaire reste un code, la somme ou l’intersection de deux codes également.
Soit \(C\) un \([n,k]\)-code sur \(\F_q\).
Définition
Le sous-code pair de \(C\) est le code \(C^0=\set{c\in C, \sum c_i=0}\). Si \(C\neq C^\circ\), \(C^\circ\) est un \([n,k-1]\) code
Le code étendu est le code
\[\overline C = \set{(x_1,\dots x_n,x_{n+1}), (x_1\dots x_n)\in C, \sum x_i=0 }\]c’est un \([n+1,k]\)-code.
Le code raccourci en la position \(n\) est le code \(\set{(c_1,\dots c_{n-1},c_n)\text{ t.q. }(c_1,\dots c_{n-1},0)\in C}\) (attention, ce n’est pas l’image de la projection, c’est la projection du noyau)
Proposition
Si \(q=2\) et \(C^\circ\neq C\), \(C^\circ\) est un \([n,k-1,d]\) code pour \(d\) pair, et un \([n,k-1,d+1]\) code pour \(d\) impair.
Démonstration
On a \(d(C)\leq d(C^0)\leq d(C)+1\). On regarde un mot de poids minimal.
Pour la dimension du sous-code pair, on utilise ce lemme qu’on va réutiliser dans le prochain paragraphe
Lemme
Soit \(E\) un \(\F_q\) espace-vectoriel de dimension \(n\), et \(\phi:E\to\F_q\) une forme linéaire. Alors
soit \(\phi\) est nulle et \(\dim\ker(\phi) = n\)
soit \(\phi\) est surjective et \(\dim\ker(\phi) = n-1\).
Code orthogonal¶
On considère le «produit scalaire usuel» \(x,y\mapsto \langle x,y\rangle=x^ty=\sum x_iy_i\) qui est une forme bilinéaire symétrique non-dégénérée sur \(\F_q^n\).
C’est-à-dire que l’on a les formules
\(\langle x+y,z\rangle = \langle x,z\rangle+\langle y,z\rangle\)
\(\langle x,y\rangle = \langle y,x\rangle\)
\(\langle ax,y\rangle = a\langle y,x\rangle\)
\(\forall y, \langle x,y\rangle = 0 \Rightarrow x=0\)
Remarque
Ce n’est pas un produit scalaire, l’axiome de définition \(\langle x,x\rangle=0\Rightarrow x=0\) est en général faux, et la positivité \(\langle x,x\rangle\geq 0\) n’a pas de sens sur \(\F_q\).
Si vous suivez...
Donner un exemple de vecteur non nul \(x\in\F_2^3\) pour lequel \(\langle x,x\rangle = 0\).
Définition
Si \(C\) est un \([n,k]\)-code, on définit son orthogonal
c’est un code (sous-espace vectoriel) de dimension \(n-k\).
Démonstration
En effet, si \(g_1,\dots g_k\) forme une base de \(C\), \(C^\bot\) est l’intersection des noyaux des \(k\) formes linéaires \(x\mapsto \langle x,g_i\rangle\) qui sont indépendantes puisque le produit est non dégénéré.
En d’autres termes, c’est le noyau de l’application surjective
Ainsi, \(C^\bot\) est un \([n,n-k]\)-code, et on a
Remarque
Une matrice vérificatrice d’un code est génératrice de son orthogonal, et vice-versa.
Attention, à la différence des espaces euclidiens (vrai produit scalaire), on n’a pas de décomposition \(\F_q^n=C\oplus C^\bot\), bien au contraire on a la possibilité suivante :
Définition
Soit \(C\) un \([n,k]\)-code, on dit que \(C\) est auto-orthogonal si \(C=C^\bot\). Cela impose que \(n=2k\) soit pair.
Le cas des codes MDS est particulièrement intéressant :
Proposition
L’orthogonal d’un code MDS est MDS.
Démonstration
Soit \(G\) une matrice génératrice d’un \([n,k,n-k+1]\) code. Par hypothèse, les mots de codes \(xG\) ont au plus \(k-1\) coordonnées nulles, donc les lignes de toute matrice extraite \(k\times k\) de \(G\) sont libres, donc la même chose est vraie de leurs colonnes, donc toute famille de \(k\) colonnes de \(G\) est libre. Or \(G\) est la matrice vérificatrice de l’orthogonal, qui est donc de distance \(\geq k+1 = n-(n-k)+1\).
Sommes de codes¶
C’est une manière pratique de construire des codes de grande distance, reposant sur le lemme suivant
Proposition
Soit \(C_1\) et \(C_2\) des codes de paramètres \([n,k_1,d_1]\) et \([n,k_2,d_2]\). Alors le code
est un \([2n,k_1+k_2,\min(2d_1,d_2)]\) code.
Démonstration
Soit \(c=(c_1,c_1+c_2)\) un mot non nul. Si \(c_2=0\), \(w(c)=2w(c_1)\geq 2d_1\). Si \(c_2\neq 0\), \(w(m)=w(c_1)+w(c_1+c_2)\geq w(c_1)+w(c_2)-w(c_1)=w(c_2)\geq d_2\) (inégalité triangulaire \(w(a+b)\geq w(a)-w(b)\), qui correspond au fait que pour annuler une coordonnée de \(c_2\) il faut qu’elle soit non nulle sur \(c_1\)). Et il existe des mots de poids \(2d_1\) et \(d_2\).
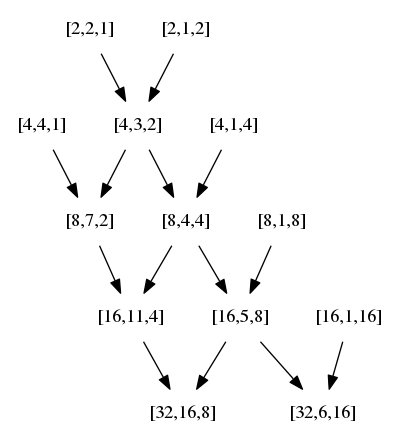
Ainsi, à partir des codes pleins \([n,n,1]\) et de répétition \([n,1,n]\) on peut construire des codes intéressants, comme les codes \([32,6,16]\) (grande distance) ou \([32,16,8]\) (taux d’information raisonnable).