Cryptographie symétrique¶
Principes¶
La théorie de Shannon montre l’existence d’un chiffre sûr : le chiffre de Vernam (one-time-pad). Sa sécurité repose sur le caractère vraiment aléatoire d’une clef aussi longue que le clair.
En pratique cependant,
on ne sait pas générer de suite vraiment aléatoire
une telle clef pose un problème de protocole : comment la transmettre de manière sécurisée…
En cryptographie symétrique, on renonce à la sécurité recommandée par Shannon, au profit d’une approche pragmatique : avoir la plus grande sécurité possible pour une clef de taille fixée à par exemple 128 ou 256 bits.
Pourquoi 128 bits ? [tot11]
On suppose donc \(\cK=\F_2^\ell\) fixé, avec par exemple \(\ell = 128\), et on suppose qu’on sait choisir de manière aléatoire un élément \(k\in\cK\).
Pour cela, deux grandes techniques :
le chiffrement par flot (stream cipher) : on construit une suite pseudo-aléatoire \(L_k:\Z\to\F_2\), et on utilise sa sortie pour pour faire un chiffre de Vernam (xor avec le clair).
le chiffrement par bloc (block cipher) : on découpe le clair en blocs de \(\ell\) bits et on applique à chacun un cryptosystème sur \(\ell\) bits.
Deux remarques préliminaires :
Dans les deux cas, les méthodes adoptées combinent deux ingrédients
un côté algébrique qui assure de la diffusion
un côté non-linéaire qui assure la confusion.
Par ailleurs la tendance en cryptographie est de prendre pour chacun de ces ingrédients un système extrèmement simple, de sorte qu’on suit les recommandations de Shannon sans y ajouter quoi que ce soit.
Attention avec le mot aléatoire :
pour faire un chiffrement par flot, on a besoin d’une séquence pseudo-aléatoire (qui ressemble à de l’aléa) mais parfaitement déterministe, puisque devant ne découler que de la clef.
pour choisir une clef (ou les paramètres d’un cryptosystème), on a besoin d’une source d’aléa forte.
Les techniques actuelles pour obtenir de l’aléa fort consistent la plupart du temps à utiliser des chiffres par blocs nourris par des compteurs et des valeurs système (heure, température du processeur).
Chiffrement par flot¶
Une variante pratique du chiffre de Vernam est donnée par les générateurs pseudo-aléatoires. La clef de chiffrement (et de déchiffrement) étant l’initialisation du générateur.
On utilise en particulier les générateurs donnés par de simples suites récurrentes linéaires d’ordre élevé : à petite échelle, elles ont des propriétés statistiques similaires aux suites aléatoires.
Une suite récurrente de degré \(d\) est une suite pour laquelle il existe des coefficients \(c_0,\dots c_{d-1}\) tels que
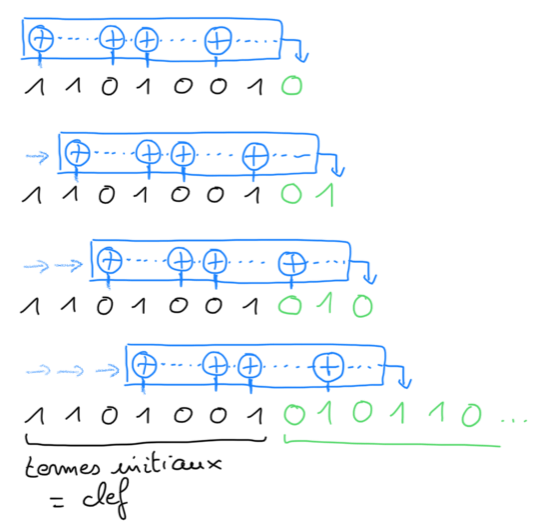
Sur le corps \(\F_2\) ces suites récurrentes sont appelées LFSR, pour Linear Feedback Shift Register : en effet on peut voir le fonctionnement par récurrence comme l’application d’un masque que l’on décale à chaque fois.
Théorème
Soit \((u_n)\in\F_2^\N\) une suite récurrente de degré \(d\). Alors
\((u_n)\) est périodique, sa période est au plus \(2^d-1\)
il existe des coefficients \(c_0,\dots c_{d-1}\) tels que pour tout choix d’initialisation \(u_0,\dots u_{d-1}\), la suite \((u_n)\) obtenue est de période \(2^d-1\).
Même si le fait que la période est grande donne des propriétés statistiques de type aléatoire à la suite, il ne faut surtout pas l’utiliser directement comme séquence pseudo-aléatoire, car il est facile de reconstruire algébriquement le polynôme minimal d’une suite récurrente.
En revanche, combiner plusieurs générateurs permet d’obtenir des suites qui résistent à l’étude.
Une technique est d’appliquer une fonction booléenne non linéaire \(f:\F_2^k\to\F_2\) aux sorties de \(k\) générateurs.
Une autre technique semble-t-il communément employée consiste à prendre trois suites récurrentes : une suite de contrôle \(C\) et deux suites de valeurs L0 et L1. La première est incrémentée à chaque tour, sa valeur détermine laquelle des deux suites L0 ou L1 est incrémentée. La sortie du générateur est la somme des sorties courantes de L0 et L1.
Remarque
Attention, des variantes simples ne fonctionnent absolument pas, comme le générateur de Geffe https://en.wikipedia.org/wiki/Correlation_attack#Breaking_the_Geffe_generator
Chiffres par blocs¶
Le message est découpé en blocs \(\F_2^l\) sur lesquels opère le chiffrement, avec \(l\) assez grand pour qu’une attaque par force brute soit impossible.
Exemples:
DES, blocs de 64 bits et clefs de 56 bits : ce n’est plus assez (DES cracker opérait en ~50h en 1998).
AES, blocs de \(l=128\) ou \(256\) bits, clef de même taille \(l\).
Modes de chiffrement¶
Soit un message \(m\) découpé en blocs \(m_i\in\F_2^l\), que l’on chiffre avec un chiffre par blocs \(e:\F_2^l\times \cK \to\F_2^l\).
Il y a plusieurs manières de procéder.
- Mode ECB
« electronic code book », blocs chiffrés indépendemment, en parallèle
\[c_i = e(m_i,k)\]de sorte que
\[m_i = d(c_i, k)\]- Mode CBC
« cipher block chaining », un bloc dépend du précédent
\[\begin{aligned} c_1 &= e(m_1, k)\\ c_i &= e(m_i + c_{i-1}, k) \text{ pour } i\gt 1. \end{aligned}\]de sorte que
\[m_i = d(c_i, k) - c_{i-1}\]- Mode CTC
On chiffre successivement les entiers \(1,\dots n\), ce qui construit un flot que l’on ajoute au message.
\[c_i = m_i + e(i,k)\]Si le cryptosystème est résistant aux attaques à clair connu cela ne pose pas de problème.
Construction du chiffre¶
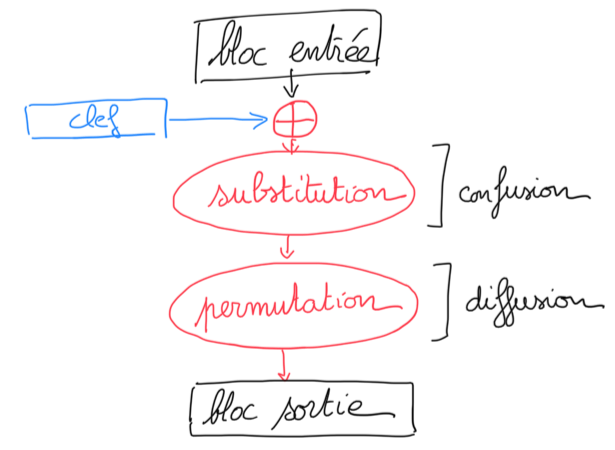
Le principe général des chiffrements par blocs est d’effectuer un certain nombre de tours d’un chiffrement élémentaire assurant les deux aspects de confusion (par l’application de fonctions non linéaires) et de diffusion (par permutation des bits), chaque tour étant paramétré par une clef de tour dérivée de la clef initiale (en général il suffit d’ajouter la clef de tour avec un xor).
Pour ces chiffres, un tour est très facile à casser, mais l’accumulation de tours rend l’analyse extrèmement difficile.
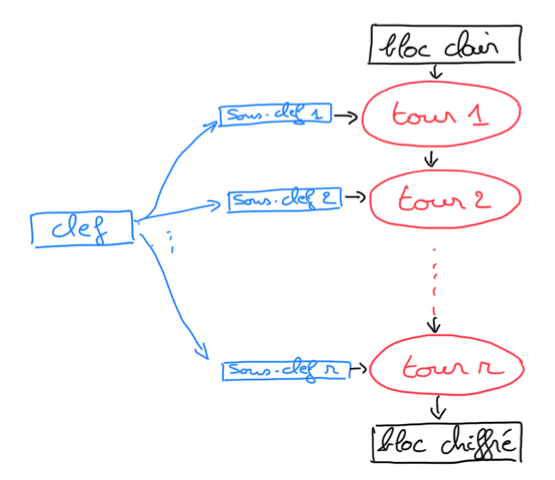
Par exemple, le chiffrement d’un bloc DES se fait par 16 tours avec des sous-clefs de 48 bits. Pour AES, c’est aussi entre 10 et 20 tours, suivant la taille des blocs (on sait casser jusqu’à 7 tours).
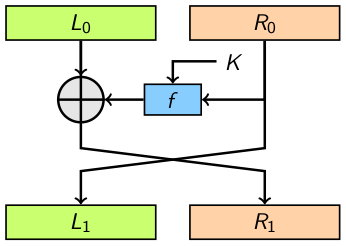
Le schéma de Feistel¶
C’est une manière commode d’obtenir un tour inversible sur 2l bits à partir d’une fonction non injective sur l bits.
Substitutions-permutations¶
Dans AES, les transformations sont toutes inversibles et obtenues par des opérations du corps \(\F_{2^8}\) : la confusion est assurée par l’inversion \(x\mapsto x^{-1}\) (substitution hautement non-linéaire), et la diffusion par l’application d’une matrice circulante sur \(\F_{2^8}^4\).