La fonction zeta¶

On fait un passage rapide sur quelques aspects fascinants de cette fonction, que l’on va retrouver dans toutes les fonctions L.

On considère la série de Dirichlet

\[\zeta(s) = \sum_n n^{-s}\]

Propriétés¶

A) produit eulérien¶

Une observation d’Euler : le théorème fondamental de l’arithmétique (tout entier s’écrit de manière unique comme produit de nombres premiers) est équivalent à l’égalité

\[\zeta(s) = \sum_n n^{-s} = \prod_p (1-p^{-s})^{-1}\]

En particulier, l’étude de zeta permet d’étudier les nombres premiers.

B) évaluation, prolongement analytique¶

A priori on peut évaluer \(\zeta(s)\) pour \(s>1\). Il se trouve que la fonction obtenue admet un prolongement méromorphe à \(\C\) tout entier.

Ce qui permet d’évaluer \(\zeta\) en d’autres valeurs. Par exemple \(\zeta(-1)=-\frac1{12}\), qu’on retrouve beaucoup sur youtube.

zeta(-1)

zeta(0)

C) équation fonctionnelle¶

Une idée géniale de Riemann a été de compléter la fonction, en ajoutant un facteur gamma

\[\gamma(s) = \Gamma_\R(s) = \pi^{-s/2}\Gamma(s/2)\]

où la fonction gamma est

\[\Gamma(s) = \int_0^\infty e^{-t}t^{s}\frac{\dt}t\]

On obtient alors la fonction complétée,

\[\Lambda(s) = \Gamma_\R(s)\zeta(s)\]

qui a une belle symétrie appelée équation fonctionnelle

\[\Lambda(s) = \Lambda(1-s)\]

D) valeurs spéciales¶

Ce sont les valeurs prises aux entiers.

[ zeta(k) | k <- [-2,-1,0/*,1*/,2] ]

Assez miraculeusement, ces valeurs ont un contenu arithmético-géométrique fort.

[ bestappr(zeta(-k)) | k <- [0..10] ]

[ bestappr( zeta(2*k) / Pi^(2*k) ) | k <- [1..5] ]

On remarque (et on démontre) deux choses remarquables

\(\zeta(2k)\in\Q\pi^{2k}\), plus précisément

\[\zeta(2k) = (-1)^{k+1}\frac{B_k}{2(2k)!}(2\pi)^{2k}\]
\(\zeta(-2k)=0\) et \(\zeta(1-2k)\in\Q\), précisément

\[\zeta(-k) = (-1)^k\frac{B_{k+1}}{k+1}\]

où les \(B_k\) sont les nombres de Bernoulli

bernvec(10)

Par ailleurs, les valeurs \(\zeta(2k+1)\), qu’on pense toutes irrationnelles, intéressent beaucoup les théoriciens des nombres (théorie des périodes).

E) bande critique, zéros¶

L’aspect le plus fascinant des fonctions L se situe dans une zone appelée bande critique.

Pour le voir, on va utiliser une représentation simplifiée des fonctions d’une variable complexe, joliment appelée « rayons x » Les fonctions méromorphes aux rayons X.

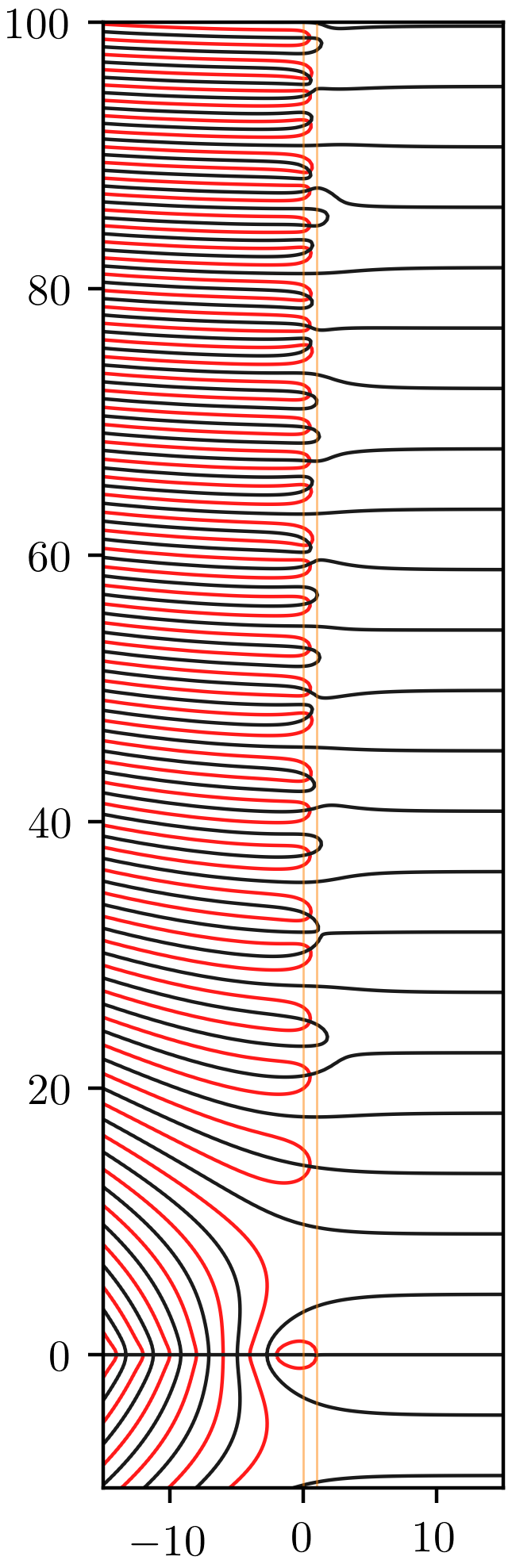
Tout le comportement intéressant est situé dans la bande critique.

En particulier ces mystérieux zéros, liés aux nombres premiers.

En pari/GP¶

zeta via lfun¶

Il y a deux implantations de la fonction zeta.

La première, qu’on a employée jusque là, utilise la formule d’Euler Mac-Laurin. Elle est très efficace pour calculer des valeurs isolées.

zeta(1+1000*I)

zeta(1+x)

La seconde consiste à utiliser le package général de fonctions L. On dispose de davantage de fonctionnalités.

lfun(1,1+1000*I)

Pour avoir la fonction L complétée,

lfunlambda(1,-3)

D’autres fonctions possibles :

lfunzeros calcule les (parties imaginaires) de zéros sur la droite critique
```
Z = lfunzeros(1,100)
```

Précalculs¶

L’algorithme d’évaluation est en deux étapes : 1. un précalcul de transformée de Fourier (de \(\Lambda(\frac12+it)\)) 2. une évaluation de série

Si on veut évaluer zeta plusieurs fois, on peut conserver l’étape 1. avec la fonction lfuninit.

Lz1000 = lfuninit(1,[1000]);

puis les évaluations sont très rapides

lfun(Lz1000, 1/2+1000*I)

lfun(Lz1000, 1/2+728*I)

lfunhardy donne la fonction sur la droite critique utilisée pour déterminer les zéros

Lz30 = lfuninit(1,[50]);
ploth(t=-50,50,lfunhardy(Lz30, abs(t))) \\ def pour t>=0

Application : zéros¶

Il y a plusieurs manières d’écrire le lien entre les nombres premiers et les zéros de la fonction zeta, au moyen de ce qu’on appelle les formules explicites.

Sans rentrer dans les détails, on donne juste une illustration numérique de ce lien.

Partons des zéros de la fonction zeta, on construit la fonction suivante

\[H(s) = 1 + \sum_\gamma \cos(\gamma \log(s) )\]

où l’on suppose que les zéros vérifient l’hypothèse de Riemann et s’écrivent \(\rho = \frac12\pm i\gamma\).

On trace les sommes partielles de \(H\), en ne considérant que les \(n\) premiers zéros.

zer = lfunzeros(1,150)
funH(s,n) = -vecsum(cos(zer[1..n]*log(s)));

Ne prenons que le premier zéro. La fonction \(cos(\gamma_1\log(s))\) oscille.

ploth(s=1.5,20,funH(s,1))

puis 2, 3, 4 zéros

ploth(s=1.5,20,funH(s,4))

ploth(s=1.5,20,funH(s,20))

Avec 50 zéros, les choses deviennent claires

ploth(s=1.5,20,funH(s,50))

Réciproquemet, partons des nombres premiers, on introduit la série suivante

\[F(t) = - \sum_{p^n} \frac{\log(p)}{\sqrt{p^n}}\cos( t\log(p^n) )\]

On calcule ses sommes partielles

funF(t,n) = {
  my(s = 0);
  forprime(p=2,n,
    my(lp = log(p));
    s += lp * sum(e=1,logint(n,p), cos( t * e * lp) / sqrt(p^e))
  ); -s;
}

ploth(t=1,30,funF(t,20))

ploth(t=1,30,funF(t,50))

ploth(t=1,30,funF(t,100))