Corps finis II¶
Soit \(L\) un corps fini de caractéristique \(p\). On note \(q=p^n\) le cardinal de \(L=\F_q\).
Proposition
Soit \(L/K\) une extension de corps finis. Il existe \(p\) premier et \(k\mid n\) deux entiers tels que \(K=\F_{p^k}\) et \(L=\F_{p^n}\).
Lemme
Soit \(L/\F_q\) une extension de corps finis. L’application \(\phi_q=x\mapsto x^q\) appartient à \(\Gal(L/\F_q)\).
Théorème
\(L/\F_q\) est galoisienne et on a un isomorphisme de groupes
Théorème
Les sous-groupes de \(\Z/n\Z\) sont les \(d\Z/n\Z\simeq \Z/(n/d)\Z\) pour \(d\mid n\). Ils sont tous cycliques.
Si \(n=\prod p_i^{e_i}\) (décomposition en facteurs premiers), alors \(n\) a \(\prod (e_i+1)\) diviseurs.
Exemple
diagramme des sous-extensions de \(\F_{2^{30}}\), donné par celui des diviseurs de \(30\).
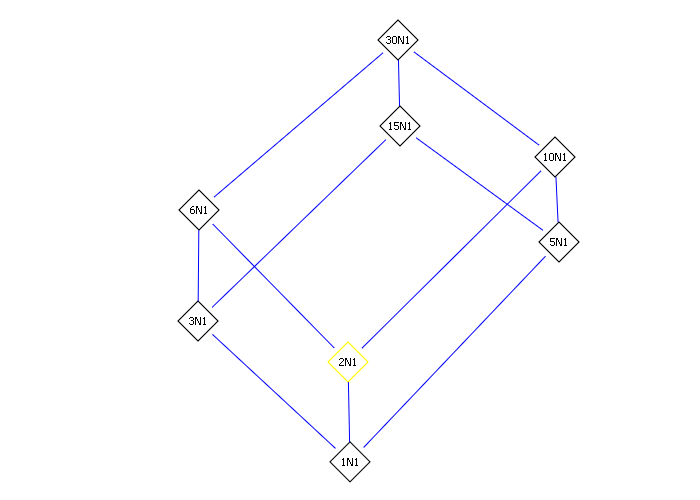
Conséquences¶
Théorème
Soit \(P\in\F_q[x]\). Alors \(P\in\F_p[x]\) si et seulement si \(P(x)^p=P(x^p)\).
Si \(P\in\F_p[x]\) irréductible de degré \(d\) a une racine \(\alpha\in\F_q\), les autres racines de \(P\) sont \(\alpha, \alpha^p,\dots \alpha^{p^{d-1}}\).
Soit \(\alpha\in\F_q^\ast\). Alors il existe \(d\) tel que \(\alpha\) est d’ordre \(p^d\) et le minimal de \(\alpha\) est \(\prod_{j<d} (x-\alpha^{p^j})\)
Corollaire
si \(\phi:\alpha\mapsto \beta\) est un morphisme de corps, les autres sont les \(\alpha\mapsto \beta^{p^k}\).